Prof.Dr.Godfried-Willem RAES
Prof.dr.Godfried-Willem Raes
Kursus: Boekdeel 4: Akoestiek , Organologie & Experimentele Instrumentenbouw,
Instrumentenleer
Hogeschool Gent : School of Arts
4020:
Pijpen en hun berekening
De hier behandelde berekeningen zijn geldig voor trillingen van luchtkolommen
in pijpen of buizen. Deze buizen kunnen zowel een ronde als een veelhoekige
doorsnede hebben. Wel moet de vorm van de doorsnede over de gehele lengte van
de pijp gelijk blijven: veelal cirkelvormig of veelhoekig. We treffen hen als
trillingsbronnen en resonatoren aan in muziekinstrumenten zoals: alle fluiten,
vele orgelpijpen, klarinetten, saxofoons, trompetten, zinken, hobos, fagotten,
tubas, serpenten... maar ook in slaginstrumenten zoals de vibrafoon en de marimba,
waar ze als resonator worden gebruikt.
Bazisgegevens:
1. Voortplantingssnelheid van het geluid in droge lucht
bij 21graden Celsius: v = 344.5 m/s
Merk op dat deze snelheid temperatuurafhankelijk
is. (zie eerdere beschouwingen terzake: v = 332 SQR(1+0.00366.T), waarin T
de temperatuur is uitgedrukt in graden Celsius)). Voorts is er nog een afhankelijkheid
van de samenstelling van de lucht (vochtgehalte, stof). Wanneer we met alle
faktoren rekening houden, blijkt dat deze snelheid in zekere mate frekwentieafhankelijk
is. Voor hele hoge frekwenties blijkt ze iets af te nemen.
2. Fundamentele vrije golflengte-formule:
f = v / l
- (f= frekwentie in Hz, v= geluidssnelheid
in m/s, l=
golflengte in meter)
- vb: een toon van 440Hz heeft een golflengte
van:
- l
= 344.5m/s / 440s^-1 = 0.783m = 78,3cm
- Merk op dat dit de fyzische lengte is van
de volledige periode van de drukgolf en dus niet de afstand tussen twee knooppunten
of twee buiken!
-
- Wil je voor een bepaalde toonhoogte weten met
welke fysische golflengte (en fysische ruimtemaat) zij overeenstemt, dan gebruik
je de formule alsvolgt:
- vb.: buis van 60cm
- f0
= 344.5m/s / 0.6 = 574 Hz
In onderstaande figuur hebben we het luchtdrukmodulatie karakter van een
geluidsgolf gepoogd weer te geven door een variabele arcering overeenkomstig
de drukvariaties in het golfverschijnsel.
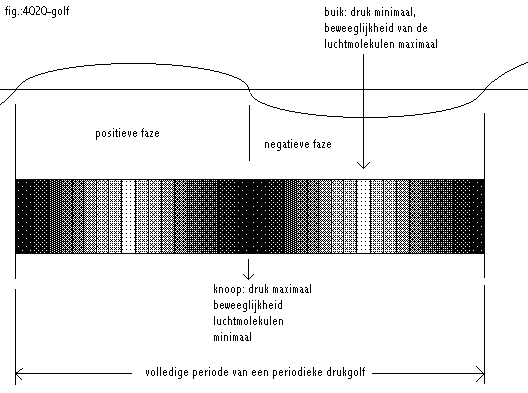
3. De toon die we zullen horen als laagste toon, wanneer we haar op
de rand van de opening aanblazen, klinkt echter een oktaaf lager! De buis resoneert
immers op een halve periode van de golflengte. Immers, aan de open uiteinden
van een buis, moet de beweeglijkheid van de lucht wel maximaal zijn (een buik),
en tussen twee buiken past een halve golflengte. De gehele golflengte is dan
ook tweemaal zolang, of, wat op hetzelfde neerkomt, de toon klinkt een oktaaf
lager. Voor de berekening van de grondtoon van een buis, moeten we dan ook onze
golflengteformule met een faktor 2 aanpassen en krijgen we:
f(0) = v / (2 l)
- Dit is de bazisformule waarvan we gebruik maken bij alle
berekeningen in verband met de akoestiek van buisachtige volumes, inklusief
rechthoekige lokalen en ruimtes. We gaan er hierbij wel van uit dat de geluidssnelheid
in de buis dezelfde is dan die in de omgeving buiten de buis. Dat is echter
alleen het geval wanneer de buisdiameter relatief groot is. Is dat niet het
geval, dan ondervindt de trillende lucht een weerstand, die de geluidssnelheid
in de buis doet afnemen.
- De hogere resonantie-frekwenties, in eerste teoretische
benadering, voor de hier beschouwde buis vindt je door nu alle halve golflengtes
te berekenen die een geheel aantal keer in deze lengte passen. Je zal vinden
dat zij -voor de hier beschouwde buis- eenvoudigweg een reeks 2, 3, 4, 5,
6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,... volgen. Of, uitgedrukt
in toonhoogte, alle gehele veelvouden van de laagste resonantiefrekwentie
of grondtoon. Dit teminste, voorzover de buis geen diameter heeft..., wat
uiteraard niet kan. Naarmate de diameter van de buis groter wordt, zullen
ook de afwijkingen van deze boventoonreeks groter worden, en dat op een bijzonder
komplexe wijze.
- Onthoudt goed dat de golflengte van de grondtoon 2 keer
de lengte heeft van de beschouwde buis.
Uitgedrukt in een eerste benaderingsformule, waarin
n het volgnummer van de boventoon weergeeft:
f(n) = n * f(0)
4. Wanneer we nu de beschouwde buis aan een kant zouden afsluiten,
dan kan aan die gesloten kant in elk geval geen trillingsbuik ontstaan, maar
slechts een knoop. De laagste resonantiefrekwentie van een buis die aan een
kant volledig is afgesloten, wordt daardoor gehalveerd in vergelijking met die
van een buis van gelijke lengte die aan beide zijden open is. Beschouwen we
nu de golflengtes die in de buis ingepast kunnen worden, dan komen we tot de
reeks 1,3,5,7,9,11,13,15,.... Of, uitgedrukt in toonhoogte, alle oneven gehele
veelvouden van de grondtoon. Ook hier weer is dit een geidealiseerd geval, omdat
de afwijkingen van deze reeks ook weer groter zullen zijn wanneer de diameter
groter wordt, en bovendien ook nog eens afhankelijk zijn van de frekwentie.
Merk op dat de golflengte van de grondtoon 4 keer de lengte
is van de beschouwde buis. (kwart-lambda resonator)
N.B.: Ook een snaar, aangeslagen
in haar middelpunt, brengt in hoofdzaak oneven harmonischen voort.
De formule voor de berekening van
de grondtoon voor een aan een kant gesloten buis is dus:
f(0) = v / (4
l)
De geidealiseerde formule voor de harmonischen reeks, waarin n
het volgnummer van de boventoon weergeeft is:
f(n) = ((2 * n)+1) * f(0)
5. Dit alles is echter (helaas of gelukkig maar?) veel te eenvoudig
om ook maar met enige werkelijkheid in precieze overeenstemming te kunnen zijn...
- In de akoestische werkelijkheid immers is het nu eenmaal
niet zo dat de resonantie van een buis precies overeenstemt met de lengte.
De drukgolf stopt immers niet aan het uiteinde van de buis. Ware dat het geval
dan zouden we trouwens ook nooit iets kunnen horen en ware de bouw van fluiten
en orgels volstrekt onmogelijk! De werkelijke trillingsbuik komt tot stand
op enige afstand van het open uiteinde van de buis. Deze afstand nu is een
funktie van de oppervlakte en de vorm van de doorsnede van de buis. De afwijking
in de werkelijke resonantiefrekwentie op grond van de vormverhoudingen van
de resonator noemt men de eindkorrektie. Zij kan empirisch en vereenvoudigd
worden berekend alsvolgt:
- Voor cilindrische buizen: akoestische buislengte
l = lengte +
(0.62 * diameter)
- Wordt er een rechte flens op de buis aangebracht dan wordt
deze faktor echter 0.82 * diameter.
-
- Aangezien de eindkorrektie zoals blijkt uit empirisch
onderzoek, mede afhankelijk is van de frekwentie, volgt hieruit dat de eindkorrektie
niet voor alle harmonischen dezelfde zal zijn! De toe te passen eindkorrektie
is evenredig met de verhouding van de diameter tot de golflengte van de beschouwde
boventoon. Het verband kan alleen in een vierde graads vergelijking benaderend
worden uitgedrukt. Het muzikaal gevolg hiervan is, dat 'juiste' boventonen
in de 3-dimensionele werkelijkheid niet kunnen bestaan en naar het rijk van
Plato's ideeen dienen te worden verwezen. Zij gelden alleen voor een buis
met diameter nul !
- A fortiori alle onzin over 'juiste boventonen' bij blaasinstrumenten
die van toongaten en kleppen zijn voorzien.
- Om de akoestiek van muziekinstrumenten -en meer bepaald
hun spektrum- te kunnen verklaren kunnen we in eerste benadering beter uitgaan
van de 'denkbeeldige' grondfrekwentie f0= v / (lengte+korrektie)
en alle veelvouden daarvan vormen dan mogelijke pieken in het opgewekte spektrum.
- De wiskunde om blaasinstrumenten op grond van hun vorm
volledig te berekenen is uiterst ingewikkeld en wordt in de praktijk zelden
toegepast in de instrumentenbouw, die in eerste plaats empirisch en pragmatisch
tewerk blijkt te gaan. Dit wil niet zeggen dat er niet berekend wordt, maar
wel, dat de bij dit rekenen gebruikte formules grotendeels empirisch tot stand
zijn gekomen en zelden op grond van afleidingen ontsproten aan de wiskunde
of de teoretische fyzika.
- De werkwijze hierbij is dat men door het bouwen van enkele
proefmodellen en het heel precies opmeten van hun eigenschappen, probeert
te komen tot geldige tabellen met maatverhoudingen tegenover geproduceerde
toonhoogte/spektrum voor reeksen instrumenten naar eenzelfde ontwerp. Dergelijke
tabellen zijn heel erg gebruikelijk in de orgelbouw, waar ze mensuurtabellen
of mensuurtafels worden genoemd. Voor elk orgelregister worden specifieke
tabellen gebruikt. Maar, zelfs de meest nauwkeurige bouwer kan er toch niet
in slagen een pijp af te leveren die met de muzikaal gewenste precizie is
gestemd, zo dat de pijp zonder verdere korrekties in het orgel kan worden
gebruikt. Ook bouwers van op buizen gesteunde blaasinstrumenten (fluiten,
klarinetten, hobos, fagotten, koperblaasinstrumenten...) zijn erg vertrouwd
met dit probleem.
- Om heel exact te zijn moeten we er echter wel op wijzen
dat er twee belangrijke faktoren zijn die maken dat het exakte gedrag van
een gebouwd muziekinstrument niet perfekt voorspelbaar is:
- a.- de onbeschikbaarheid van volledige zuiver wiskundige
beschrijvingsmodellen voor reele akoestische oscillatoren, hoewel op
dit gebied vorderingen zijn gemaakt die vooral toepassing hebben gevonden
in acoustical modelling, een betrekkelijk nieuwe syntezetechniek,
die een wiskundig model van een trillend fysisch objekt gebruikt als
generator in software.
- b.- de principiele fouten die bij elke empirische
meting aanwezig zijn, waardoor een gebouwd instrument steeds een kummulatieve
fout zal vertonen waardoor het verschillend is van een ander 'identiek'
geproduceerd exemplaar.
- Met 'normale' precieze handwerktuigen kunnen we een buis
van bvb. 60cm deze lengte geven met een fout van +/-0.1mm. Dit wil dus zeggen
dat 20 dergelijke buizen van 60cm onderling tot 0.2mm in lengte kunnen verschillen.
Wanneer voor de positie van de toongaten bvb. bij een fluit, alweer -per gat-
een fout mogelijk is stel eveneens +/-0.1mm, en wanneer deze foutmarge eveneens
van toepassing is op de diameter van de buis..., dan zal je makkelijk inzien
dat de afgewerkte instrumenten onderling meer dan 1% dimensionele verschillen
kunnen vertonen. Wanneer je je aan de bouw van instrumenten waagt, is het
dan ook van het grootste belang precies te bepalen wat de fout is die het
gebruik van de meettoestellen en werktuigen die je ter beschikking hebt, met
zich brengt. Het heeft geen enkele zin berekeningen uit te voeren met een
precizie die die van het praktisch haalbare te boven gaan. In de werkplaats
van de niet werkelijk gespecialiseerde instrumentenbouwer, moet je de fout
op metingen en versnijdingen begroten op 5% tot hooguit 1%, dit voor de meest
zorgvuldigen onder ons.
6. De geluidsdruk voortgebracht door
een aangeblazen pijp is (bij gelijkblijvende winddruk) een funktie van de diameter
van de pijp. Dat is volkomen logisch omdat naarmate de diameter groter is, er
ook meer lucht tot trillen zal worden gebracht. Dat orgelpijpen een grotere
diameter hebben naarmate de tonen lager worden, is een gevolg van onze gehoorkarakteristiek
die nu eenmaal minder gevoelig is voor lagere tonen dan voor die die met het
spraakgebied overeenkomen. Merk op dat wanneer de diameter van een pijp wordt
vergroot, ook de grootte van de toe te passen eindkorrektie toeneemt. De vergroting
van de diameter heeft bovendien ook een invloed on het spektrum of de klankkleur.
Volgende grafische voorstelling van open en gesloten pijpen en de wijze waarop
de lucht erin in resonantie kan trillen, moge een en ander duidelijk maken:
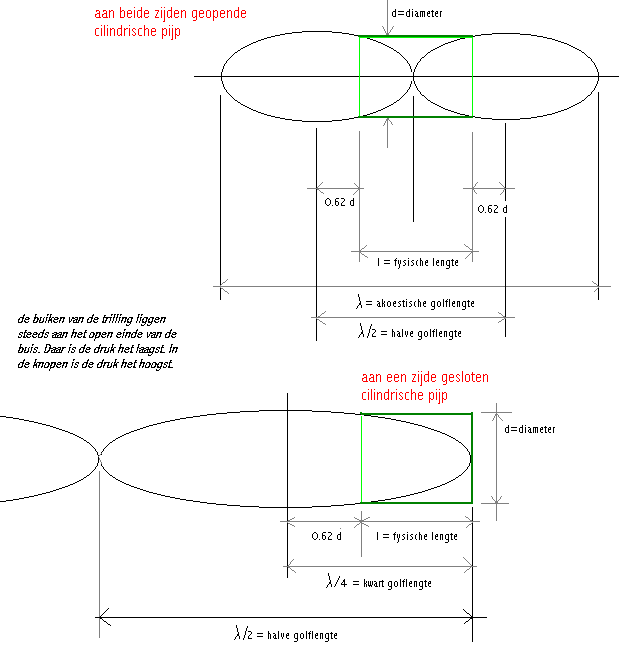
Terwille van de duidelijkheid hebben we wel de verhouding diameter tot lengte
van de buis erg sterk overdreven.
7. Wanneer de
pijp konisch wordt gemaakt, blijven bovenstaande formules ten dele geldig. De
harmonischen-reeks voor konische pijpen bestaat net zoals voor open cyclindrische
pijpen, bij benadering uit alle gehele veelvouden van de laagste resonantiefrekwentie.
Echter wanneer we het extreem geval bekijken van een pijp die uitloopt op een
punt, dan komt de resonantiefrekwentie overeen met die van een open pijp. Naarmate
we nu het kleine gat vergroten -waarbij we het gat wel goed afgesloten houden!-
, zakt de resonantietoon geleidelijkaan tot en met een geheel oktaaf. In dit
geval gedraagt de konische pijp zich zoals een cilindrische die aan een kant
is gesloten.
De berekeningen voor perfekt konische en aan een kant gesloten cylindrische
pijpen voor 4 frekwenties zijn weergegeven in volgende illustrerende tabel:
| Frekwentie |
cyclindrische pijp |
konische pijp |
| 55 Hz |
151 cm |
302 cm |
| 110 Hz |
75 cm |
151 cm |
| 220 Hz |
38 cm |
38 cm |
| 880 Hz |
9 cm |
19 cm |
Door het spelen met het vormverloop van een pijp, kan worden bereikt dat een
maximum aantal boventonen binnen een gegeven stemming 'juist' kunnen worden
gespeeld. Daarop berust de techniek van de bouwer van koperblaasinstrumenten.
In de volgende tekeningen hebben we het gedrag van gesloten konische pijpen
gevisualiseerd:
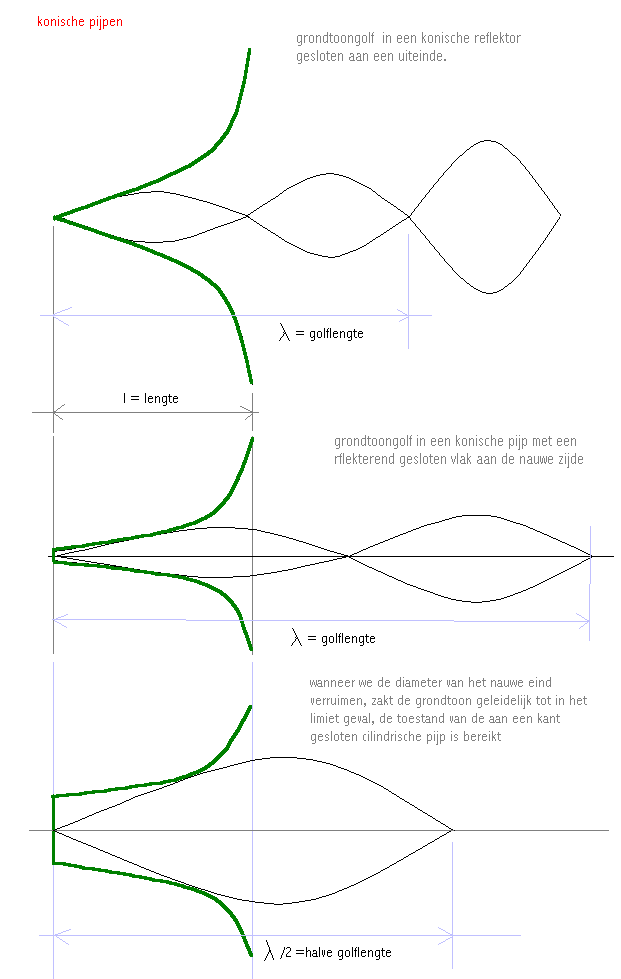
Een gangbare formule voor de berekening van de resonantiefrekwentie van gestopte
konische pijpen tekenden we uit alsvolgt:
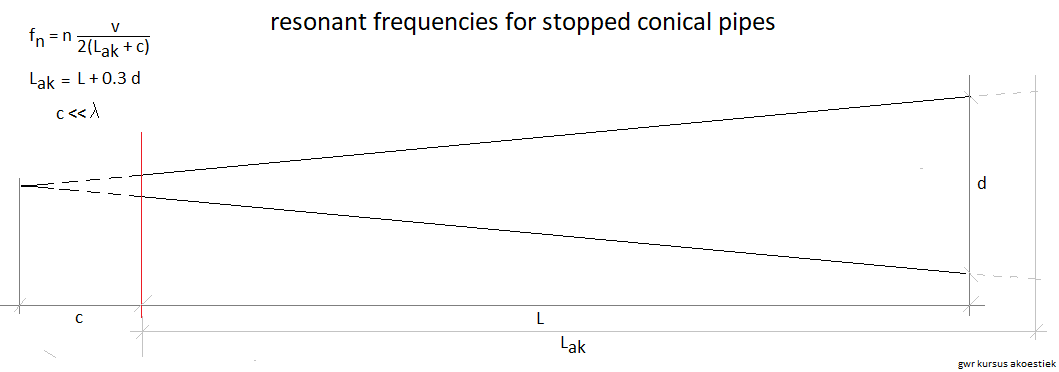
De lengte getekend als c en aangeduid met de vertikale rode lijn, is
niet fysisch aanwezig maar is de denkbeeldige voorzetting van konus. Voorwaarde
voor de toepasbaarheid van deze formule is wel dat de lengte c veel kleiner
moet zijn dan de golflengte van de berekende frekwentie.
Eigen onderzoek inzake conische pijpen met een kleine openingshoek -dus waarvoor
aan de konditie C << lambda zeker niet is voldaan leverde volgend resultaat
op:
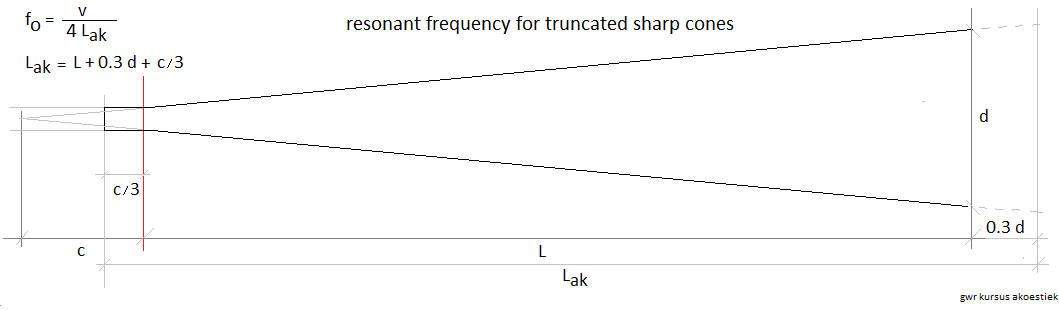 Merk op dat
we hier uitkwamen op kwart golflengte pijpen. De boventoonreeks verloopt -met
kleine afwijkingen- als een reeks 1,2,3,4,5.... Dergelijke conische resonatoren
pasten we toe in een van onze membraanorgel automaten:
<3Pi>. Daar zijn ook alle onderzoeksgegevens terug te vinden.
Merk op dat
we hier uitkwamen op kwart golflengte pijpen. De boventoonreeks verloopt -met
kleine afwijkingen- als een reeks 1,2,3,4,5.... Dergelijke conische resonatoren
pasten we toe in een van onze membraanorgel automaten:
<3Pi>. Daar zijn ook alle onderzoeksgegevens terug te vinden.
8. het aangeblazen uiteinde van een
pijp (koperblaasinstrumenten) gedraagt zich als een gesloten uiteinde. Dat is
intuitief goed in te zien: immers daar moet de druk wel groot zijn. Het aangeblazen
uiteinde van een fluit daareentegen, moet worden beschouwd als een open uiteinde.
Ook dat kan intuitief worden ingezien, aangezien het toongat van de fluit met
veel wind wordt aangeblazen. De luchtbeweging is er maximaal, de druk dus laag.
Dit geldt eveneens voor kernspleetfluiten.
Voorbeelden van konische instrumenten zijn hobos en fagotten. De klarinet daareentegen
is voor het grootste deel van haar boring cilindrisch en gedraagt zich grotendeels
als een aan een kant gesloten pijp.
Wanneer het vormverloop van de pijp afwijkt van het zuiver cilindrische of
het konische, dan worden de eigenresonanties minder uitgesproken , wat zich
uit in een moeilijker intoneerbaarheid en een meer inharmonisch spektrum van
het instrument. In sommige instrumenten wordt uitgerekend dit gezocht: de australische
didgereedoo dankt er zijn specifieke klankkleur aan.
Enkele eenvoudige berekeningsvoorbeelden en vraagstukken:
1.- Vraag: We willen een open buis hebben met een toonhoogte van 440Hz bij
een temperatuur van 21 graden celsius. We willen daarvoor PVC buis gebruiken
met een binnendiameter van 0.0285m. Welke lengte moeten we afzagen op precies
bij 440Hz uit te komen?
- geluidssnelheid bij T=21 graden: v = 332 * SQR(1+0.00466.T) = 344,5m/s
- gewenste akoestische golflengte voor 440Hz: l=
v/f = 344,5 / 440 = 0.783m
- de buis is aan beide kanten open en bevat een halve golf, dus 0.391 m
- hiervan moeten we tweemaal de eindkorrektie aftrekken: 2 (0.62 * 0.0285)
= 0.035m
0.391m - 0.035m = 0.356m
Wanneer we deze buis nu aan een kant dichtmaken, dan zakt de toon tot:
- de akoestische lengte komt nu overeen met een kwart golf en wordt nu: l
+ 0.62d, of 0.356 + (0.62 * 0.0285) = 0.373 waarbij de gehele akoestische
golflengte nu overeenkomt met het viervoudige hiervan, of: 1.495m .
- de frekwentie wordt nu: f = 344.5/ 1.495 = 230.4Hz
Je ziet meteen dat het interval heel wat kleiner is dan een oktaaf!
Inharmoniciteit van de trillingen in luchtkolommen
Kundt kwam -reeds in de 19e eeuw- langs experimentele weg tot volgende bevindingen,
die voor de praktijk van de instrumentenbouw en voor een goed begrip van de
oorzaken van inharmoniciteit in trillende luchtkolommen, wel degelijk een belangrijke
betekenis hebben:
- a. De snelheid van het geluid in een buis neemt af wanneer de diameter ervan
afneemt. Vanaf een bepaalde diameter echter, is de geluidssnelheid in de buis
dezelfde van die gemeten daarbuiten, in de omringende lucht.
- b. De mate waarin de geluidssnelheid afneemt in funktie van afnemende diameter
van de buis, neemt toe met de golflengte van de toon.
- c. verontreinigingen (stof en poeder) in de buis met kleine diameter, verminderen
de geluidssnelheid nog verder.
- d. wanneer het oppervlak van de buis ruwer wordt gemaakt, daalt ook de geluidssnelheid.
Naarmate de diameter toeneemt, is dit effekt geringer.
- e. In buizen met grote diameter is de geluidssnelheid onafhankelijk van
de amplitude, maar wanneer de diameter afneemt, neemt de geluidssnelheid weer
toe met toenemende geluidsdruk.
(Vertaling door onszelf, en geciteerd in Rayleigh, "The
Theory of Sound", volume 2,p.59, oorspronkelijk gepubliceerd in 1896. Kundt
publiceerde zijn resultaten reeds in 1868. )
Bevinding a kan proefondervindelijk aangetoond worden met een eind transparante
slang in zacht PVC passend in de boring van een klarinet of saxofoonmondstuk.
De voortgebrachte grondtoon is 'infrasoon' en lijkt in geen verband te staan
met de fysische lengte van de slang. Luister ook eens goed naar de tonen die
verkregen worden bij overblazen...
Bevinding b, maakt dat de boventoonreeks van een buis alvast zeker niet harmonisch
kan zijn. Zelfs de oktaven zijn te klein. Voor gangbare pijplengte en diameter
verhoudingen mogen we er gerust van uitgaan dat vanaf de 10e boventoon, we mijlen
verwijderd zijn van een harmonische reeks. Vanzodra de diameter van de buis
niet meer te verwaarlozen is tegenover de golflengte van de beschouwde boventoon,
is de inharmoniciteit zelfs niet eens meer geleidelijk, maar vertoont zij een
slingerend gedrag.
Bevinding d is van belang voor het verklaren van het verschil in toon bij klarinetten
en hobo's gemaakt uit hout enerzijds en gepolierde kunststof anderzijds.
Filedate: 970928/ updated 2022-02-28




 Merk op dat
we hier uitkwamen op kwart golflengte pijpen. De boventoonreeks verloopt -met
kleine afwijkingen- als een reeks 1,2,3,4,5.... Dergelijke conische resonatoren
pasten we toe in een van onze membraanorgel automaten:
Merk op dat
we hier uitkwamen op kwart golflengte pijpen. De boventoonreeks verloopt -met
kleine afwijkingen- als een reeks 1,2,3,4,5.... Dergelijke conische resonatoren
pasten we toe in een van onze membraanorgel automaten: