
Dr.Godfried-Willem RAES
Kursus Experimentele Muziek: Boekdeel 1: Algoritmische Kompositie
Hogeschool Gent: Departement Muziek en Drama
Naar inhoudtafel kursus
"Fuzzy Logic"
Of, 'Vage logika', zoals deze titel, in het Nederlands vertaald, zou kunnen luiden. Maar, sinds het begrip fuzzy onvertaald in alle wereldtalen -inkluzief het japans- werd overgenomen, werd het tot een begrip op zich binnen het domein van elektronische regeltechnieken en software-systemen.
Klassieke booleaanse operatoren maken zoals we weten gebruik van niet meer dan twee logische toestanden: waar of vals, 1 of 0. Ontelbaar echter zijn in de werkelijke wereld de omstandigheden waarin een bewering niet zomaar eenduidig als waar of vals kan worden geklasseerd: bvb. het is warm weer, de batterij is leeg, de student kent zijn leerstof, de dissonantie van een interval... immers het kan ook 'aan de warme kant zijn' of, de batterij kan ook niet meer als nieuw zijn, of voor een bepaald doel nog wel bruikbaar, de student kan gapende gaten in zijn kennis hebben, maar bepaalde andere zaken dan weer bijzonder goed beheersen enz...
Algemeen gesteld, de toeschrijving van een eigenschap aan een veranderlijk verschijnsel, is slechts zelden een kwestie van eenduidig waar of vals. Beslissingsregels die gebruik maken van scherpe 0-1 overgangen blijken in de praktijk vaak een te abrupt gedrag te vertonen wanneer ze worden gebruikt in cybernetische systemen (regelsystemen met feedback). Onderstel bvb. dat we een regelsysteem voor de snelheid van een auto of trein willen ontwerpen. Wanneer we de gewenste maximum snelheid willen beperken tot 120km/u, dan zouden we natuurlijk kunnen een regelkring kunnen opzetten alsvolgt:
- stel Vmax=120km/u
- meet snelheid en plaats haar in v
- vergelijk v met Vmax
- IF v > Vmax THEN Rem
Dit soort regeling heeft het nadeel dat ze voor overgangen tussen 0-1 sterke neigingen tot oscilleren kent: de rem wordt snel aan en uit gezet, wat niet bevorderlijk is voor een soepele rijstijl.
Vanzelfsprekend kan met de klassieke booleaanse algoritmiek het regelsysteem -o.m. door het invoeren van hysteresis- verbeterd worden. Het aantal te formuleren regels neemt dan echter heel snel toe. Principieel echter blijven het steeds 'bewijsbare' systemen. Vooral het ontbreken van een garantie inzake deze laatste formele eigenschap, heeft vele logici en wiskundigen sceptisch gemaakt tegenover fuzzy-systemen.
STAP 1:
Deze fuzzy regelsystemen nu, vertrekken van de idee dat elke eigenschap geacht wordt in een bepaalde mate op een verschijnsel (parameter) van toepassing te zijn. Die mate kan worden uitgedrukt als een getal tussen 0 en 1 (de griekse mu wordt hiervoor in de technische literatuur vaak gebruikt). Dit proces noemt met de fuzzyfikatie van de input(s). Deze input(s) zijn numerieke gevektorizeerde waarden. In de Engelse vakliteratuur noemt met hen 'crisp-values': eenduidig bepaalde numerieke waarden, dit in tegenstelling tot 'fuzzy-values' die bij de verwerking van de inputs worden gebruikt.
De mate waarin een eigenschap (fuzzy-value) aan een parameter (crisp-value) kan worden toegeschreven, kan nu voor elke eigenschap die met betrekking tot de betreffende parameter als relevant kan worden beschouwd vastgelegd worden in een voor elke eigenschap specifieke kurve. Veronderstel dat we voor een parameter vier eigenschappen menen te moeten en kunnen onderscheiden, dan zou dit kunnen leiden tot vier verschillende kurves:

De bepaling van deze kurves is een louter empirische aangelegenheid. In vele gevallen zullen we te maken krijgen met de klokkurves (Gauss) uit de statistiek, maar ook driehoeken, trapeziums en zelfs kurves met rechthoekige segmenten zijn mogelijk. Ter beperking van de komplexiteit van de berekeningen, worden voor in dedicated systems geimplementeerde fuzzy- systemen vooral driehoek-kurves toegepast (lineaire flanken kunnen algoritmisch verkregen worden door eenvoudige inkrementeringen met een positieve of negatieve konstante)
Wie iets met fuzzy algoritmiek wil gaan programmeren in een kompositorische toepassing, beveel ik sterk het gebruik van beta-kurves aan. (cfr. het betreffende hoofdstuk). Uiteraard dienen we alleen eigenschappen te bepalen voor zover we die nodig menen te hebben voor de bepaling van de uiteindelijke output. De kurves moeten in elk geval op voorhand in look-up tables worden vastgelegd.
Voor elke waarde van de crisp-parameter, bestaan er nu -na aflezing van de mu-waarden in de kurves- vier mu-waarden. Grafisch kunenn we deze waarden aflezen door een vertikale lijn te trekken voor de waarde van de parameter en te zien op welk punt van de kurve deze lijn de kurve raakt. In ons voorbeeld levert dit volgend rezultaat op:
parameter = 80
eigenschap 1 = 0
eigenschap 2 = 0
eigenschap 3 = 0.03
eigenschap 4 = 0.4
Merk op dat, bij veralgemening, de som der mu waarden ook groter kan zijn dan 1, dat met eenzelfde parameterwaarde meer dan 1 eigenschap in dezelfde mate kan overeenkomen enzomeer! De procedure en denkwijze vertoont een grote verwantschap met de verzamelingenleer en de Venn- diagrammen uit de moderne wiskunde en leent zich heel goed voor een grafische representatie. Een software implementatie hiervoor zal bij voorkeur gebruik maken van a priori in een array geplaatste look-up tables. De kurves zelf moeten dan immers slechts eenmalig berekend en in het geheugen geplaatst worden. Bij wijze van voorbeeld, zouden we ons kunnen voorstellen dat de inputparameter hier de snelheid van een handbeweging is. Deze snelheid (input-parameter) heeft dan vier mogelijke (vage) eigenschappen:
eigenschap1 = traag
eigenschap2 = rustig
eigenschap3 = levendig
eigenschap4 = snel en zenuwachtig
Wanneer de snelheid 80 is, zoals in ons voorbeeld, dan heeft de beweging de eigenschappen snel en zenuwachtig evenals levendig. Op grond van de kurves hoort deze snelheid immers in beide verzamelingen, maar in verschillende mate, thuis.
STAP 2:
De tweede stap, na de fuzzyfikatie van de inputs, bestaat er nu in ook de output(s) (outputparameters) middels fuzzyfikatie vast te leggen. De kurves waarmee de outputparameters worden vastgelegd lopen niet geheel gelijk aan die voor de inputs. Hier is het immers van groot belang de centrale waarden goed te bepalen ('centroids', pivoteerpunten, kantelpunten, zwaartepunten...). Elke centroide kurve heeft ook hier X en Y (of mu)waarden, maar -in een eerste introduktie- is vooral de X-waarde is hier van belang. Veronderstellend dat we 3 output-eigenschappen in de hand willen houden, dan bepalen we nu voor elke eigenschap een kurve met een centrale waarde (centroid-value). Bij deze waarde moet mu = 1. Anders gesteld, voor minstens 1 waarde dient de eigenschap duidelijk te zijn gedefinieerd.
Zoals stap 1, hoeft ook deze stap niet in 'real-time' te gebeuren, maar worden alle variabelen op voorhand berekend en in look-up tables geplaatst.
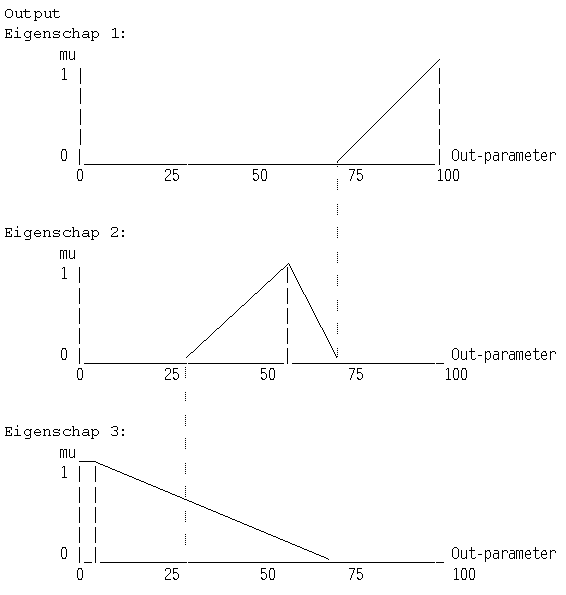
Alweer bij wijze van voorbeeld, zouden we ons kunnen voorstellen dat de outputparameter hier de toonhoogte van een geluid is. Het doel van het fuzzy-systeem zou dan kunnen zijn, deze toonhoogte op een soepele wijze te regelen met de eigenschappen van de beweging van onze hand. De semantische invulling wordt dan:
Output-Parameter = toonhoogte (bvb. midi-noot)
Out-Eigenschap1 = hoog (bvb. midi-noot 127)
Out-Eigenschap2 = middelmatig (bvb. midi-noot 60)
Out-Eigenschap3 = laag (bvb. midi-noot 12)
Overlappingen van de kurves spelen hebben hier geen enkel effekt. Ook gaten tussen de outputkurves kunnen hier, in tegenstelling tot de input- kurves- geen kwaad aanrichten. De onderlinge plaatsing van de centrale waarden zijn van determinerend belang voor de vorm van de klok-kurve die door de uiteindelijke output-parameter waarde, na stap 3, zal worden gevolgd.
STAP 3:
De derde stap in het proces, bestaat er nu in een verzameling regels samen te stellen waarmee op grond van de eigenschappen van de input, de eigenschappen van de output worden bepaald. Dit wordt geformuleerd middels uitdrukkingen die ons bekend zijn uit Basic:
IF ... THEN ...
waarbij dan de operatoren:
AND (intersektie)
OR (unie)
NOT (komplement)
kunnen worden toegevoegd. Er zijn minstens evenveel regels nodig als er eigenschappen zijn in de input-fuzzy-verzameling. Dit tenminste voorzover je alle mogelijke inputkondities wil behandelen. Om de output-funktie een gladder verloop te geven, is het vaak wenselijk meer regels te bepalen, of, want dat blijkt in de praktijk vaak een gelijkaardig effect te sorteren, de centroid-waarden voor de output-eigenschappen een beetje te verschuiven.
Na het IF statement komen bepalingen van fuzzy-waarden voor de input: bvb.
IF eigenschap1 AND eigenschap3 THEN Out-eigenschap1 = NOT(True)
IF eigenschap2 OR eigenschap3 THEN Out-eigenschap3 = True
etc...
De toewijzing van True of False aan de output-eigenschappen bepaalt welke out-eigenschap kurves we zullen gebruiken bij de berekening van de output- parameter waarde. De formulering van de regels volgt vrij nauw de wijze waarop we de werking van het systeem in woorden zouden beschrijven. De goede werking van het systeem staat of valt uiteraard met de juistheid van deze beschrijving. Vergeet ook niet, dat elke keer we het regelsysteem toepassen, de Out- eigenschap waarden False moeten zijn!.
Laten we dit even proberen voor ons voorbeeld:
'Reset-values:
Out-eigenschap1= False
Out-eigenschap2= False
Out-eigenschap3= False
'Apply rules:
IF eigenschap1 THEN Out-eigenschap3= True
IF eigenschap2 THEN Out-eigenschap2= True
IF eigenschap3 THEN Out-eigenschap2= True
IF eigenschap4 THEN Out-eigenschap1= True
Het effekt van dit regelsysteem zal zijn dat de toonhoogte toeneemt met de bewegingssnelheid. In ons voorbeeld (cfr. stap1) stelden we dat eigenschappen 3 en 4 van toepassing waren. Toepassing van de hier bepaalde regels heeft dus voor gevolg dat nu de Out-eigenschappen 1 en 2 waar zullen zijn, terwijl Out- eigenschap3 niet van toepassing is (False).
STAP 4:
Het proces waarbij nu de waarde van de outputparameter eenduidig wordt bepaald, noemen we de defuzzyfikatie. Hierbij wordt de (crisp) output vastgelegd in funktie van een weging van alle out-eigenschappen die voor de gegeven input van kracht zijn.
In ons voorbeeld:
De input behoorde voor 3% tot de eigenschap 3 Ún voor 40% tot de eigenschap 4. (Wegingsfaktoren 0.03 en 0.4).
De centrale waarden voor de out-eigenschappen die van toepassing zijn waren (stap 2): 60 (Out-Eigenschap2) en 127 (Out-eigenschap1)
De output parameter waarde wordt nu als een gemiddelde berekend alsvolgt:
OE2 = out-eigenschap 2 - centrum-waarde (60)
OE3 = out-eigenschap 3 - centrum waarde (127)
mu3 = fuzzy-waarde voor eigenschap 3 (0.03)
mu4 = fuzzy-waarde voor eigenschap 4 (0.4)
Out-parameter = (OE2 * mu3) + (OE3 * mu4) / (mu3 + mu4)
of, numeriek uitgewerkt voor ons voorbeeld:
Midi-noot = (60 * 0.03) + (127 * 0.4) / (0.03 + 0.4)
= 1.8 + 50.8 / 0.43
= 52.6 / 0.43
= 122
De hele fuzzy-beslissingsprocedure leidt dus in het geheel niet tot 'vage' of onbepaalde uitkomsten, maar geeft juist eenduidige (crisp) uitkomsten voor 'vage' inputgegevens. nDe omzettingformule, geformuleerd in haar algemeenheid (voor n-input parameters, elk met m eigenschappen en voor i-output parameters met elk j eigenschappen) is:
Veranderlijken:
N = aantal input parameters
M = aantal input eigenschappen
I = aantal output parameters
J = aantal output eigenschappen
byte(n) = waarde van de input parameters 0->N
M(n) = aantal eigenschappen gedefinieerd voor elke input parameter 0->N
J(i) = aantal eigenschappen gedefinieerd voor elke output parameter 0->I
Mu(n,m,byte(n)) : n= input-parameter pointer 0->N
m= parameter-eigenschap pointer 0->M
Uc(i,j): i= output-parameter pointer 0->I
j= parameter-eigenschap pointer 0->J
In Uc wordt de centrum-waarde geplaatst.
Formule:

Deze formule kan eenvoudig in enkele programmalussen worden geprogrammeerd. Wanneer we de nul-termen (niet aangesproken eigenschappen) op voorhand weglaten, dan omvat de bewerking, op de finale deling na, slechts optellingen en vermenigvuldigingen, wat door de komputer vrij snel kan worden afgehandeld. Dat de kompleksiteit heel snel toeneemt in funktie van het aantal parameters en eigenschappen blijkt duidelijk. Overigens verbeterd dit meestal niet de overdrachtkarakteristiek. We doen er goed aan zo weinig mogelijk parameters en eigenschappen te definieren en elk koppel dat niet wezenlijk bijdraagt tot de overdrachtkarakteristiek kunnen we maar beter geheel elimineren.
Een kompleks fuzzy systeem wordt eerder opgebouwd door een verhoging van het aantal binnen het systeem werkzame fuzzy-algoritmes dan door het verhogen van het aantal parameters/eigenschappen binnen deze algoritmes.
In de praktijk der regelsystemen is fuzzy-logic bijzonder goed toepasbaar gebleken en het praktisch belang ervan is vele mate groter dan dat van bvb. de zogenaande neurale netwerken. Fuzzy-logic wordt de laatste tijd overigens ook meer en meer in de hardware van de schakelingen zelf geimplementeerd. Er zijn zelfs integrale fuzzy mikroprocessoren op de markt. De achterliggende algoritmiek biedt onnoemelijk vele perspektieven voor de muzikale kompositie: niet alleen voor toepassingen waarbij real-time inputs worden gebruikt, maar ook voor louter kompositorische beslissingsprocedures.
Fuzzy-logic maakt gebruik van een 'knowledge-base': immers de op voorhand opgegeven kurves waarmee de eigenschappen worden toegekend moeten gezien worden als 'kennis' van het systeem. In die zin vormt Fuzzy- logic een deel van wat men 'artificial-intelligence' noemt. We kunnen ook werkelijk kennisverwervende systemen bouwen met fuzzy-logic, wanneer we bvb. onze kurves tijdens een leerfaze van het programma interaktief zouden vastleggen, of wanneer we de centrum-waarden van de output-eigenschappen zouden bepalen vanuit een feedback beoordeling op grond van de globale overdrachtfunktie.
Aanbevolen verdere literatuur m.b.t. fuzzy-logic:
'Circuit Cellar', #56, March 1995 : Tema-nummer over dit onderwerp met verschillende bijdragen van verschillende auteurs.
SCHOLTEN, Henk: "Regelen met Fuzzy Logic en PID", Ed.:Elektuur, Beek, 1992, ISBN: 90-5381-020-X
Terug naar inhoudstafel kursus: <Index kursus>
Ter verduidelijking van de werking van fuzzy-systemen schreven we een eenvoudig programma waarin zo'n systeem werd geimplementeerd. Uitgegaan wordt van een systeem met 4 inputs en 4 outputs. Voor elk input worden 5 eigenschappen bepaald, en voor elke output 3 eigenschappen.
' **************************************************************************
' * FUZZY.BAS *
' * demonstration program for fuzzy logic *
' * Dr.Godfried-Willem RAES *
' **************************************************************************
' 19.03.1995: First sketch - very inefficiently coded
' good for gaining insight in Fuzzy's internals... But..., it works!
REM $DYNAMIC
CONST NrInParams = 3: 'aantal input parameters -1
CONST NrUitParams = 3: 'aantal output-parameters -1
CONST NrInProps = 4: 'aantal eigenschappen per input parameter -1
CONST NrUitProps = 2: 'aantal eigenschappen per output parameter -1
CONST InParamRange = 127: 'bereik van de input-waarden
CONST UitParamRange = 127: ' bereik van de output-waarden
CONST False = 0
CONST True = 1
COMMON SHARED Mu!(), Uc%(), UitLogic%() :' not essential
DECLARE FUNCTION ADC% (channel%) : ' dummy-function
DIM SHARED Mu!(0 TO NrInParams, 0 TO NrInProps, 0 TO InParamRange)
DIM SHARED Uc%(0 TO NrUitParams, 0 TO NrUitProps)
' we gebruiken in Uc% alleen de ene waarde waarvoor Mu = 1
DIM SHARED UitLogic%(0 TO NrUitParams, 0 TO NrUitProps)
DIM TellerOutbyte!(0 TO NrUitParams)
DIM NoemerOutbyte!(0 TO NrUitParams)
DIM Outbyte%(0 TO NrUitParams)
DIM Prop!(0 TO NrInParams, 0 TO NrInProps)
' de kurves worden ingelezen uit twee ascii-files:
FI$ = "C:\BC7\ELEKTRON\FUZZYIN.DAT"
FO$ = "C:\BC7\ELEKTRON\FUZZYOUT.DAT"
CLS
LOCATE 1, 10
PRINT " FUZZY-LOGIC 4-in 4-out DEMONSTRATION PROGRAM ";
LOCATE 25, 10
PRINT " Written by Dr.Godfried-Willem RAES - 19.03.1995 ";
' set-up the fuzzy-algorithm:
STAP1:
'*****
' bepaal de eigenschappen - deze staan in een in te lezen databestand met naam FI$: "FUZZYIN.DAT" (ASCII file)
OPEN FI$ FOR INPUT AS #1
DO: ' lees-lus voor FI$
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Parameter" OR EOF(1)
IF EOF(1) THEN EXIT DO
INPUT #1, i%: ' nummer van de parameter (0- NrInParams)
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Property"INPUT #1, j%: ' nummer van de eigenschap (0 - NrInProps)
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Dataset"
INPUT #1, elements%: ' aantal ingevulde -en volgende- waarden-koppels
FOR n% = 0 TO elements% - 1
INPUT #1, k%: ' parameter-waarde
INPUT #1, m!: ' fuzzy-coefficient
Mu!(i%, j%, k%) = m!
' for debugging purposes:
LOCATE 3, 10
PRINT "Reading Input Fuzzy-data set..."
LOCATE 4, 10
PRINT "Par="; i%, "Prop="; j%, "Val="; k%, "Fuz="; m!; " ";
NEXT n%
LOOP UNTIL EOF(1)
CLOSE #1
' merk op dat alle niet in de data-file opgenomen waarden, gewoon op NUL blijven.
STAP2:
'*****
OPEN FO$ FOR INPUT AS #1
WHILE NOT EOF(1)
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Parameter"
INPUT #1, i%: ' nummer van de parameter (0- NrOutParams)
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Property"
INPUT #1, j%: ' nummer van de eigenschap
DO
INPUT #1, dummy$
LOOP UNTIL dummy$ = "_Centroid"
INPUT #1, Uc%(i%, j%)
' for debug only:
LOCATE 5, 10
PRINT "Reading Fuzzy output centroid values";
LOCATE 6, 10
PRINT i%, j%, Uc%(i%, j%); " ";
WEND
CLOSE #1
STAP3:
'*****
DO
' vanaf hier begint de werkelijke fuzzy-machine te werken: reset eerst de logische waarden voor de uitgangseigenschappen:
FOR n% = 0 TO NrUitParams
FOR m% = 0 TO NrUitProps
UitLogic%(n%, m%) = False
NEXT m%
NEXT n%
' get input data:
FOR i% = 0 TO NrInParams
byte%(i%) = ADC(i%): ' lees bvb. ADC-kanalen met een funktie
LOCATE 7, 10 + (i% * 16) PRINT "byte"; i%; "="; byte%(i%),
NEXT i%
' bepaal voor de gegeven input-parameters de van kracht zijnde eigenschap: kopieer daartoe de Mu waarde voor het betreffende byte in een array Prop!()
FOR i% = 0 TO NrInParams
FOR j% = 0 TO NrInProps
Prop!(i%, j%) = Mu!(i%, j%, byte%(i%))
' for debug:
LOCATE 8 + j%, 10 + (i% * 16)
PRINT "Mu="; Prop!(i%, j%); " ";
NEXT j%
NEXT i%
' de formulering van de regels kan uiteraard niet zonder semantiek... het hier gegeven voorbeeld is dan ook eerder arbitrair:
IF Prop!(0, 0) THEN UitLogic%(0, 0) = True
IF Prop!(0, 1) THEN UitLogic%(0, 1) = True
IF Prop!(0, 2) THEN UitLogic%(0, 1) = True
IF Prop!(0, 3) THEN UitLogic%(0, 1) = True
IF Prop!(0, 4) THEN UitLogic%(0, 2) = True
IF Prop!(1, 0) THEN UitLogic%(1, 0) = True
IF Prop!(1, 1) THEN UitLogic%(1, 1) = True
IF Prop!(1, 2) THEN UitLogic%(1, 1) = True
IF Prop!(1, 3) THEN UitLogic%(1, 2) = True
IF Prop!(1, 4) THEN UitLogic%(1, 2) = True
IF Prop!(2, 0) THEN UitLogic%(2, 0) = True
IF Prop!(2, 1) THEN UitLogic%(2, 1) = True
IF Prop!(2, 2) THEN UitLogic%(2, 1) = True
IF Prop!(2, 3) THEN UitLogic%(2, 1) = True
IF Prop!(2, 4) THEN UitLogic%(2, 2) = True
IF Prop!(3, 0) THEN UitLogic%(3, 0) = True
IF Prop!(3, 1) THEN UitLogic%(3, 1) = True
IF Prop!(3, 2) THEN UitLogic%(3, 2) = True
IF Prop!(3, 3) THEN UitLogic%(3, 2) = True
IF Prop!(3, 4) THEN UitLogic%(3, 2) = True
STAP4:
'*****
' Defuzzyfikatie en bepaling van de outputparameters
' **************************************************
'reset outvalues:
FOR n% = 0 TO NrUitParams
TellerOutbyte!(n%) = 0
NoemerOutbyte!(n%) = 0
Outbyte%(n%) = 0
NEXT n%
' voer de sigma-formule uit, voor de teller:
FOR n% = 0 TO NrUitParams
FOR m% = 0 TO NrUitProps
FOR i% = 0 TO NrInParams
FOR j% = 0 TO NrInProps
IF (Prop!(i%, j%)) AND (UitLogic%(n%, m%)) THEN
TellerOutbyte!(n%) = TellerOutbyte!(n%) + (Uc%(n%, m%) * Prop!(i%, j%))
END IF
NEXT j%
NEXT i%
NEXT m%
NEXT n%
' herhaal voor de noemer:
FOR n% = 0 TO NrUitParams
FOR i% = 0 TO NrInParams
FOR j% = 0 TO NrInProps
IF (Prop!(i%, j%) > 0) THEN
NoemerOutbyte!(n%) = NoemerOutbyte!(n%) + Prop!(i%, j%)
END IF
NEXT j%
NEXT i%
NEXT n%
' bereken de rezultaten:
FOR n% = 0 TO NrUitParams
IF NoemerOutbyte!(n%) THEN
Outbyte%(n%) = TellerOutbyte!(n%) / NoemerOutbyte!(n%)
END IF
' Display result:
LOCATE 21, 10
PRINT "Output-bytes:";
LOCATE 22, 10 + (n% * 16)
PRINT "Out"; n%; "="; Outbyte%(n%),
NEXT n%
LOOP UNTIL INKEY$ = "*"
END
REM $STATIC
FUNCTION ADC% (channel%)
' dit is een dummy
x = RND(1) * 127
ADC% = x
END FUNCTION
Ter illustratie geven we ook de inhoud van de voor de demonstratie gebruikte data-files:
1. De input kurves: "FUZZYIN.DAT"
' Data-file for 'Fuzzy-bas'
' *************************
' Input-gegevens
_Parameter , 0
_Property , 0
_Dataset , 10
0, 1,1, 0.9,2, 0.8,3, 0.7,4, 0.6,5, 0.5, 6, 0.4,7, 0.3,8, 0.2,9, 0.1
_Parameter , 0
_Property , 1
_Dataset , 19
7, 0.1,8, 0.2,9, 0.3,10, 0.4,11, 0.5,12, 0.6,13, 0.7,14, 0.8,15, 0.9,16, 1,17, 0.9,18, 0.8,19, 0.7,20, 0.6,21, 0.5,22, 0.4,23, 0.3, 24, 0.2,25, 0.1
_Parameter , 0
_Property , 2
_Dataset , 19
10, 0.1,11, 0.2,12, 0.3,13, 0.4,14, 0.5,15, 0.6,16, 0.7,17, 0.8,18, 0.9,19, 1, 20, 0.9,21, 0.8,22, 0.7,23, 0.6,24, 0.5,25, 0.4,26, 0.3,27, 0.2,28, 0.1
_Parameter, 0
_Property, 3
_Dataset, 30
27, 0.05,28, 0.1,29, 0.2,30, 0.3,31, 0.4,32, 0.5, 33, 0.6, 34, 0.7, 35, 0.8, 36, 0.9, 37, 1, 38, 1, 39, 1, 40, 1, 41, 1, 42, 1, 43, 1, 44, 1, 45, 1, 46, 1,47, 1,48, 0.9,49, 0.8,50, 0.7,51, 0.6,52, 0.5,53, 0.4,54, 0.3,55, 0.2,56, 0.1
_Parameter, 0
_Property, 4
_Dataset, 80
50, 0.05, 51, 0.1, 52, 0.2, 53, 0.3, 54, 0.4, 55, 0.5,56, 0.52,57, 0.53,58, 0.54,59, 0.55,60, 0.56,61, 0.57,62, 0.58,63, 0.59,64, 0.60,65, 0.61, 66, 0.62, 67, 0.63, 68, 0.64,
69, 0.65, 70, 0.66, 71, 0.67, 72, 0.68,73, 0.69,74, 0.70,75, 0.71,76, 0.72,77, 0.73,78, 0.74,79, 0.75,80, 0.76,81, 0.78,82, 0.79,83, 0.80,84, 0.81,85, 0.82,86, 0.83,87, 0.84,88, 0.85,89, 0.860,90, 0.870,91, 0.873,90, 0.874,91, 0.875,92, 0.876,93, 0.877,94, 0.878,95, 0.879,96, 0.880,97, 0.881,98, 0.882,99, 0.884,100, 0.885,101, 0.886,102, 0.887,103, 0.888,104, 0.889,105, 0.890,106, 0.892,107, 0.894,108, 0.896,109, 0.898,110, 0.899,111, 0.90,112, 0.91,113, 0.92,114, 0.93,115, 0.94,116, 0.96,117, 0.98,118, 0.99,119, 0.992,120, 0.994,121, 0.996,122, 0.997,123, 0.998,124, 0.999,125, 1,126, 1,127, 1
_Parameter, 1
_Property, 0
_Dataset, 10
0, 1,1, 0.9,2, 0.8,3, 0.7,4, 0.6,5, 0.5,6, 0.4,7, 0.3,8, 0.2, 9, 0.1
_Parameter, 1
_Property, 1
_Dataset, 19
7, 0.1, 8, 0.2,9, 0.3, 10, 0.4,11, 0.5,12, 0.6,13, 0.7,14, 0.8,15, 0.9,16, 1,17, 0.9,18, 0.8,19, 0.7,20, 0.6,21, 0.5,22, 0.4,23, 0.3,24, 0.2,25, 0.1
_Parameter, 1
_Property, 2
_Dataset, 19
10, 0.1,11, 0.2,12, 0.3,13, 0.4,14, 0.5,15, 0.6,16, 0.7,17, 0.8,18, 0.9,19, 1,20, 0.9,21, 0.8,22, 0.7,23, 0.6,24, 0.5,25, 0.4,26, 0.3,27, 0.2,28, 0.1
_Parameter, 1
_Property, 3
_Dataset, 30
27, 0.05,28, 0.1,29, 0.2,30, 0.3,31, 0.4,32, 0.5,33, 0.6,34, 0.7,35, 0.8,36, 0.9,37, 1,38, 1,39, 1,40, 1,41, 1,42, 1,43, 1,44, 1,45, 1,46, 1,47, 1,48, 0.9,49, 0.8,50, 0.7,51, 0.6,52, 0.5,53, 0.4,54, 0.3,55, 0.2,56, 0.1
_Parameter, 1
_Property, 4_Dataset,80
50, 0.05, 51, 0.1,52, 0.2,53, 0.3,54, 0.4,55, 0.5,56, 0.52,57, 0.53,58, 0.54,59, 0.55,60, 0.56,61, 0.57,62, 0.58,63, 0.59,64, 0.60,65, 0.61,66, 0.62,67, 0.63,68, 0.64,69, 0.65,70, 0.66,71, 0.67,72, 0.68,73, 0.69,74, 0.70,75, 0.71,76, 0.72,77, 0.73,78, 0.74,79, 0.75,80, 0.76,81, 0.78,82, 0.79,83, 0.80,84, 0.81,85, 0.82,86, 0.83,87, 0.84,88, 0.85,89, 0.860,90, 0.870,91, 0.873,90, 0.874,91, 0.875,92, 0.876,93, 0.877,94, 0.878,95, 0.879,96, 0.880,97, 0.881,98, 0.882,99, 0.884,100, 0.885,101, 0.886,102, 0.887,103, 0.888,104, 0.889,105, 0.890,106, 0.892,107, 0.894,108, 0.896,109, 0.898,110, 0.899,111, 0.90,112, 0.91,113, 0.92,114, 0.93,115, 0.94,116, 0.96,117, 0.98,118, 0.99,119, 0.992,120, 0.994,121, 0.996,122, 0.997,123, 0.998,124, 0.999,125, 1,126, 1,127, 1
_Parameter ,2
_Property, 0
_Dataset, 10
0, 1,1, 0.9,2, 0.8,3, 0.7,4, 0.6,5, 0.5,6, 0.4,7, 0.3,8, 0.2,9, 0.1
'... enzovoort tot alle parameters en eigenschappen gebruikt in het programma zijn ingevuld... ( de data files zijn beschikbaar in de klas).
De file voor de outputparameters en eigenschappen ziet eruit alsvolgt:
' Data file for Fuzzy-outputs in FUZZY.BAS
' ****************************************
' Values filled in for demonstration purposes only
_Parameter , 0
_Property , 0
_Centroid , 15
_Parameter , 0
_Property , 1
_Centroid , 60
_Parameter , 0
_Property , 2
_Centroid , 127
_Parameter , 1
_Property, 0
_Centroid,15
_Parameter, 1
_Property, 1
_Centroid, 60
_Parameter, 1
_Property, 2
_Centroid,127
_Parameter,2
_Property,0
_Centroid,15
_Parameter,2
_Property,1
_Centroid,60
_Parameter,2
_Property,2
_Centroid,127
_Parameter,3
_Property,0
_Centroid,15
_Parameter,3
_Property,1
_Centroid,60
_Parameter,3
_Property,2
_Centroid,127
Filedate: 950329/9709
Terug naar inhoudstafel kursus: <Index kursus>
Naar homepage Dr.Godfried-Willem RAES