Dr.Godfried-Willem RAES
Kursus Experimentele Muziek: Boekdeel 1: Algoritmische kompositie
Hogeschool Gent : Departement Muziek & Drama
| <Terug naar inhoudstafel kursus> | sampleratekonversie |
1150:
Tot hiertoe hebben we ons in de vorige hoofdstukken eigenlijk alleen beziggehouden met de 'makro-komponenten' van de muziek: haar toonhoogtestrukturering, haar ritmiek en algemene samenhang. Niet echter met de aard van wat er op mikro-temporeel vlak in de muziek aan de hand is en kan zijn. Hier echter willen we dit domein, dat namelijk van het inwendige van de klank zelf, gaan verkennen. Dit uiteraard met het oog op het beheersen ervan teneinde het ook kompositorisch en analytisch te kunnen aanwenden.
Het gebied van de algoritmische kompositie kan inderdaad worden omschreven als bestaande uit drie duidelijk onderscheidbare gebieden, waarbij elk gebied ook nog zowat zijn eigen specialisten en zijn eigen 'invisible colleges' -om met Thomas Kuhn te spreken- kent. Elk van die gebieden heeft eigen publikaties in verschillende tijdschriften, ze houden andere colloquia en hebben centra rond verschillende universiteiten hogescholen en instellingen. Ook historisch onstonden ze op een ander ogenblik. In historische volgorde zijn alvolgt te omschrijven:
1.- Algoritmiek van de muzikale syntax
2.- Algoritmiek van de muzikale klank (klanksinteze)
3.- Algoritmiek van de muzikale uitvoering (real-time & interaktieve algoritmiek)
Daarbij moeten we eigenlijk nog een gebied vermelden dat evenwel voor de komponist van minder belang is:
4.- Algoritmiek van de muzikale analyze
Dit laatste gebied -dat we hier volledigheidshalve vermelden- behoort tot de wetenschappelijke en experimentele muzikologie en poogt via algoritmische technieken in ruime zin (o.m. gebruik makend van wiskundige statistiek en de ervan afgeleide technieken zoals neurale netwerken en fuzzy logic) strukturele verbanden te vinden (dus eigenlijk ook algoritmen) in bestaande muzikale produkten. Het is een gebied dat o.m. binnen de onderzoeksgroep aan het IPEM (Universiteit Gent) intensief wordt ontwikkeld.
Tot nu toe hebben we in deze syllabus eigenlijk uitsluitend aandacht besteed aan de eerstgenoemde en oudste aanpak van algoritmisch komponeren. Het is van de drie genoemde ook de enige die geen zware eisen stelt aan de apparatuur en aan de programmeervaardigheid van de komponist. Immers, een kompositieprogramma hoeft niet in ';real-time' te lopen. Ook met goed leesbare, inzichtelijke maar niet helemaal efficiente kode, kan hier dus zinnig werk worden geleverd. Anders echter is het gesteld wanneer we ons op algoritmische wijze willen gaan bezighouden met de interne wetmatigheden van klanken en geluiden. Daarvoor waren tot voor enkele jaren DAC's en ADC's nodig gekoppeld aan snelle geheugentoegang uiterst efficiente verwerkingskode en speciale processoren (DSP's). De hierin geinteresseerde komponist zal meestal niet over een voldoende technische achtergrond beschikken om zich op dit terrein te begeven, hoewel het niet moet uitgesloten worden. Er is echter -zoals we verder zullen zien- toch licht aan het eind van de tunnel. Immers de opgang van goede klankkaarten en speciale audiochips geintegreerd op Pentium MMX moederborden gekoppeld aan het beschikbaar komen van een binnen Windows geintegreerde API, maakt het ons vandaag mogelijk ook dit gebied ten volle te ontsluiten en te integreren binnen onze kompositorische aktiviteit.
Ook aan de derde algoritmische mogelijkheid willen we in deze kursus uiteraard ruime aandacht besteden.
Maar nu eerst...:
Klanksinteze: de interne kompositie van een klank
A. Akoestische en wiskundige grondslagen
Zonder daar in deze kursus al te ver te moeten op ingaan is het erg belangrijk enkele fundamenteel veschillende methodes te onderkennen die kunnen worden gebruikt voor het synthetisch genereren van klanken en klankkleuren.
Klankkleur en klankkleurverandering in het verloop van een klank zijn verschijnselen die nogal wat korrelatie vertonen met wat men de golfvorm noemt van die klank. Die golfvorm is nooit die van de klank zelf, maar wel die van zijn elektrisch equivalent, zoals dat wordt verkregen hetzij na omzetting van een akoestische klank via een mikrofoon in een analoog verlopend elektrisch signaal, hetzij sintetisch, door de toevoering van het elektrisch opgewekt signaal aan een luidspreker. Er kleven overigens nogal wat problemen aan de associatie klank-golfvorm en meer bijzonder klankkleur- golfvorm. Een van de grootste bezwaren tegen het koncept, is dat van geen enkel akoestisch geluid, de golfvorm konstant is. Bovendien is ook de periodetijd , bekeken op micro-schaal, van periode tot periode verschillend. Het grootste probleem van de geluidssynthese zit precies in deze faktoren die men al te vaak, ter vereenvoudiging, buiten beschouwing laat, verscholen.
Steunt op een wiskundige/akoestische teorie volgens dewelke elke periodieke golfvorm moet worden beschouwd als zijnde samengesteld uit een (oneindig...) aantal harmonische boventonen (en evt. ondertonen of subharmonischen) die trillingsgetallen hebben die veelvouden zijn van een bepaalde grondfrekwentie.
Deze theorie kan, zoals de meeste in dit gebied, wanneer we een hoop wiskunde willen vermijden, nog het eenvoudigst grafisch worden verduidelijkt. De tak van de wiskunde die zich met het analyseren van periodieke trillingen (niet alleen muzikale!) bezighoudt noemt men de Fourier-analyze, waarover we in de kursus akoestiek meer vertellen.
Het volgende DOS Basic-programma tekent op het komputerscherm het resultaat van het additief synthetiseren van een golf vanuit twee sinussen. De samenstellende sinussen worden resp. bovenaan en helemaal onderaan het scherm getekend, terwijl het resultaat in het midden komt te staan. In de menu-keuze mogelijkheden moet uiteraard wel de optie additieve synthese worden gekozen. De andere mogelijkheden worden verder besproken. Het programma laat echter een eenvoudige vergelijking toe tussen het resultaat van de diverse klanksynthese mogelijkheden.
SCREEN 0START:INPUT "X-input frekwentie ? (neem heel kleine waarden)",
FXINPUT "Y-input frekwentie ?", FYPRINT "Gewenste overdrachtfunktie ? : "PRINT "A= multiplier sin x.t * sin y.t - FM-synthese ringmodulator
" ' product synthesis FMPRINT "B= difference of squares - FM-synthese
worteltrekking" ' vector differencePRINT "C= addition sinx.t + sin y.t - Additieve
synthese " 'additive synthesisINPUT " KEUZE ? ", K$SCREEN 3 ' pas de screen-mode aan aan je eigen komputerPI = 3.1415926#HX = 2 * PI * FXHY = 2 * PI * FYHXR = (HX * PI) / 180HYR = (HY * PI) / 180FOR T = 0 TO 699: 'horizontale as ( tijdsas) voor Hercules-video
cardA = SIN(HXR * T)C = A * 10'teken de x-frekwentie sinus bovenaan
het schermLINE (T, C + 10)-(T + 1, C + 10)B = SIN(HYR * T)D = B * 10teken de y-frekwentie sinus onderaan
het schermLINE (T, D + 300)-(T + 1, D + 300)SELECT CASE UPPER(K$)CASE IS "B": UO= ((A^2) - (B ^ 2)) * 20 +
150CASE is "A": UO = (A * B * 20) + 150CASE IS "C": UO = ((A + B) * 20) + 150CASE ELSE: GOTO STARTEND SELECT' teken de sinus op het scherm: [DRAWSIN]:LINE (T, UO)-(T + 1, UO)NEXT T'wanneer de golfvormen getekend zijn
stop het programma - 'je verlaat het door eender welke toets
in te drukkenDO : LOOP UNTIL INKEY$<> ""EIND:SCREEN 0ENDKlassieke additieve synthese-algoritmen pogen dus klankkleuren te zien als optelsommen van periodieke sinusgolven -eventueel (meestal zelfs) met onderlinge fazeverschuivingen- met eigen specifieke amplitudes. Wiskundig ziet dit eruit alsvolgt:
Ut= A0*Sin(1*x0*t + h0) + A1*Sin(2*x0*t + h1) + A2*Sin(3*x0*t+h2) + A3*Sin(4*x0*t+h3)+....
Het uitgangssignaal wordt gevormd door een permanente som, waarin t de tijdsfunktie is (van 0 tot ....), A0, A1,A2,A3... de amplitudes van de verschillende boventonen, de reeks 1*x0, 2*x0, 3*x0,4*x0 de frekwenties van de harmonischen (gehele veelvouden van x0, de grondfrekwentie) en -optioneel- de reeks h0 ,h1,h2,h3,h4... de fazehoek van de betreffende harmonische tegenover de grondfrekwentie. Dit kan ook worden geschreven onder gebruikmaking het komplekse getallen (cfr. boekdeel 2 voor een opfrissing van de kennis terzake) als:
| µ
Ut= S a(n) COS(2p nf(0)t) + b(n) SIN(2p nf(0)t) n=-µ |
of, wanneer we stellen
A(n)=a(-n) + a(n)
en
B(n)=b(n)-b(-n)
en rekening houdend met het feit dat
COS(x)=COS(-x)
SIN(x)=-SIN(-x)
Dan krijgen we:
| ¥
U(t)= A(0)/2 + S A(n). COS(2.p .n.f(0).t) + B(n). COS(2.p .n.f(0).t) n=1 |
Hierin zijn de coefficienten A(n) en B(n) de Fourier coefficienten voor de reele en de imaginaire spektraalkomponenten (harmonieken) in het tijdsdomeinsignaal Ut.
In de meest primaire implementaties van additieve synthesealgoritmen worden de amplitudeverhoudingen tussen de diverse boventonen in de loop van de tijd konstant gehouden. Het is precies in de konstantheid van die verhoudingen dat de specificiteit van een klankkleur -volgens dit paradigma- besloten ligt.
Toen men na veel praktisch experimenteel werk vond dat op deze wijze gemaakte klanken toch niet konden tippen aan die uit de akoestische werkelijkheid, begon men te experimenteren met een variabele fazeverschuiving tussen de harmonischen.
In latere additieve algoritmen zette men het hele koncept op losse schroeven, door ook de amplitudes als tijdsfunkties op te vatten en zelfs, door af te zien van het idee van de harmonischen als gehele veelvouden van een grondfrekwentie. Het spektralisme is hieruit voortgekomen.
Bij volledige veralgemening kwam men zo tot additieve synthesealgoritmen waarbij klanken werden opgebouwd uit een willekeurig (machinebeperking...) aantal bij elkaar opgetelde spektraalkomponenten waarvan zowel de frekwenties, als de amplitudes en de faze funkties werden van de tijd. Dat de komplexiteit op die wijze exponentieel de hoogte in gaat wordt duidelijk vanzodra je het veralgemeend algoritme poogt in een programmeerbaar algoritme onder te brengen...
Hiervan bestaan nogal wat varianten: PWM, PPM, PCM ... afkortingen die respektievelijk staan voor PulsWidthModulation , PulsePositionModulation en PulsCodeModulation.
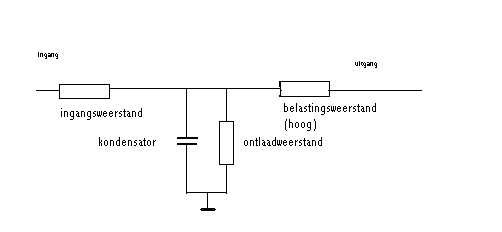
Om deze vormen van klanksynthese te begrijpen, kunnen we best uitgaan van een zuiver elektronisch - zij het dan sterk vereenvoudigd - koncept. Veronderstel een kondensator met een eraan parallel geschakelde weerstand, gevoed via een andere in serie geplaatste weerstand:

Stel nu dat we aan deze schakeling volgende reeks van pulsen met gelijke hoogte (amplitude) waarvan de breedte (de duur dus) in verhouding staat tot de momentane waarde van het door ons gewenste spanningsniveau , toevoeren :
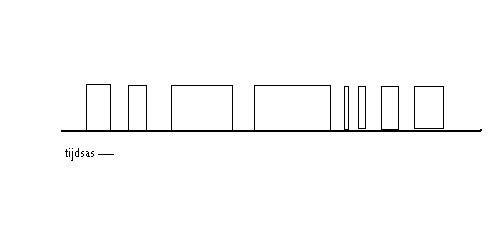
Wanneer de puls hoog is , wordt de kondensator bijgeladen. Dit bijladen gaat net zolang door als de puls hoog blijft. Uiteraard kan de lading nooit hoger worden dan de hoogte van de puls. Er is dan ook een maximale pulsbreedte. Omgekeerd, wanneer er geen puls is ( niveau is laag) , ontlaadt de kondensator zich over de weerstand , net zolang als de puls laag blijft. De spanning op de uitgang weerspiegelt dan ook doorlopend het gemiddelde van de ladingen over de kondensator. De kondensator met de eraan parallel geschakelde weerstand gedraagt zich immers zo'n beetje als een lekkende emmer. De afgevlakte golfvorm die we aan de uitgang van de schakeling kunnen waarnemen zal dan ook (ongeveer, vanwege mijn beperkt tekentalent met de muis...)verlopen alsvolgt:
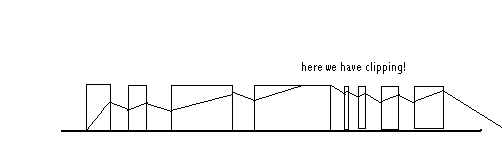
Het zal (hopen we...) duidelijk zijn , dat het mogelijk is door een juist afmeten van de pulsduur , eender welke golfvorm te bereiken. Het ligt ook erg voor de hand om bij deze vorm van synthese een beroep te doen op een komputersysteem dat de pulsen kan genereren.
Op pulsbreedtemodulatie bestaan in de praktijk nog tal van varianten . Het is immers ook mogelijk, in plaats van zoals hier de pulsbreedte te moduleren in funktie van de gewenste momentane amplitude , de puls zelf steeds even breed te houden , maar zijn positie in de tijd te gaan moduleren (PPM). Ook kunnen de pulsen worden gebruikt als drager van louter binaire informatie, waarbij ze dan een seriele getallensequens vormen, die dan echter aan een DAC moet worden toegevoerd voor demodulatie. Dit systeem wordt o.m. toegepast in de compact disc en in de DAT cassetterecorder.
PWM heeft als grootste voordeel zijn geweldige eenvoud. Er is welhaast geen hardware voor nodig. Je kan op je eigen PC bvb. zonder veel omhaal experimenteren met een 8-stemmige synthesizer door elk van de databits als PWM-out bit te programmeren. De enige noodzakelijke hardware is de integrator op de uitgangen, eventueel nog gevolgd door een low-pass filtertje. (cfr.boekdeel 2).
Parentesis:
Dat een komputer ook zonder dat er enig soort syntesizer aan te pas komt in staat is klanken op te wekken zal iedereen die al ooit op een PC heeft gewerkt wel bekend zijn. De beep-toontjes die bij het opstarten worden produceerd, de tonen die worden geproduceert binnen heel wat software, om de gebruiker attent te maken op fouten of onjuiste invoer van gegevens en de muziekjes die heel wat komputerspelletjes, zonder aanwezigheid van een Soundblaster-kaart o.i.d., begeleiden zijn daarvan triviale voorbeelden.
De eenvoudigste wijze om aan de komputer een toon te ontlokken, bestaat erin een enkel bit van een bepaald I/O of geheugenadres, met de periodiciteit overeenkomend met de gewenste toonhoogte om te schakelen. De signaalgeleider overeenkomend met het betreffende bit kan dan kwazi rechtstreeks met een luidspreker worden verbonden en tot geluid worden omgetoverd...
Wanneer de timer-funktie in bovenstaand voorbeeld per duizendste van een sekonde telt, dan zal de toon gedurende precies 1 sekonde klinken. De toonhoogte in dit voorbeeld zal echter een rechtstreekse funktie zijn van de snelheid van de kombinatie komputer-kompiler en zal dus aan onze kontrole ontsnappen. Om ook deze toonhoogte te kunnen bepalen, moeten we het programma van een tweede tijd-instruktie voorzien:
In dit voorbeeld bepaalt tijdslus (2) hoe lang bit0 op adres &H350 laag blijft en tijdslus (3) hoe lang het bit hoog blijft. In dit voorbeeld kan de periodetijd dus worden berekend als de som van beide tijdsintervallen: 10 + 10 = 20 ms. De verkregen toonhoogte zal dus 1/20ms = 50Hz zijn.
Bepalen we nu nieuwe variabelen A, B, C als resp. de duur van de toon, de laag-tijd en de hoog-tijd, dan is het mogelijk louter via software een toon te genereren met programmeerbare klankkleur (bepaald door de verhouding tussen B en C) en tijdsduur (bepaald door A).
Het klankopwekkingsprogramma wordt dan:
Nog steeds gebruik makend van eenzelfde I/O of geheugenadres is het mogelijk volgens hetzelfde systeem onze klankopwekking over meerdere kanalen tegelijk te laten verlopen, door elk bit op analoge wijze te gaan schakelen.
Hoewel dit teoretisch volkomen korrekt is, kleven er praktisch gezien nogal wat bezwaren aan een dergelijke 1-bits metode van klankopwekking, tenminste wanneer we haar met behulp van een doordeweekse PC zouden willen toepassen. Een simpele berekening moge dit verduidelijken:
Onderstel dat we voor muziek tonen tot en met 20000 Hz willen opwekken, dan zal de som van de variabelen B en C dus kleiner dienen te zijn dan
2.5 E-5 + 2.5 E-5 = 5 E-5
(dit is 50 microseconden) en het oplossend vermogen van de timer-funktie dus hoogstens 25 microsekonden. Willen we dit bereiken voor een volledig byte, en dus voor 8 kanalen, dan wordt dit reeds 3.125 microseconden. Aangezien echter de komputer nog heel wat tijd nodig heeft om de overige instrukties en funkties in het programma uit te voeren dienen we dit getal nog minstens door een faktor 25 per kanaal te delen, waarmee we op 0.0156 microsekonden uitkomen. De PC zal dus minstens een klokfrekwentie moeten hebben in de orde van de 64MHz, een waarde die zowat op de grens ligt van wat haalbaar is met de huidige PC technologie. (66MHz is anno 1993 het maximum voor een 80486 PC). Hierbij werd dan nog helemaal geen rekening gehouden -en dit zal uiteindelijk de beslissende faktor zijn- met de rekentijd die de komputer nodig heeft om deze geluiden dan binnen een te genereren muzikaal verloop op te wekken, iets waarvoor een kompositiealgoritme nodig is en evenmin met de toch wenselijke 'user-interface' waarmee we allicht onze digitale klankgenerator zullen willen uitrusten. Wanneer echter geen hoge kwalitatieve eisen aan het opgewekte geluid worden gesteld, is deze methode bruikbaar en vindt ze ook wel toepassingen, bvb. voor pulsbreedte sturing van elektromechanische onderdelen zoals bvb. gebruikt in player-pianos.
Zouden we voorts FM-syntese (zie verder) willen implementeren met de hierboven geschetste methode van klankopwekking, dan hebben we alle 8-kanalen nodig voor de opwekking van een enkele klank opgebouwd uit 8 FM komponenten. De som van alle bits wordt dan aan de luidspreker toegevoerd.
Een volledig 32-stemmige digitale syntesizer geimplementeerd met geschakelde I/O of geheugenplaatsen, zou dan een klokfrekwentie dienen te hebben van:
32 * 64MHz = 2.048 GHz
Dit is zelfs met de snelste Cray mainframe onmogelijk. Gelukkig zijn er ook andere wegen mogelijk om tot het gewenste resultaat, nml. digitale klanksynteze, te komen. De PC laten we daarbij echter alleen die dingen doen waar hij echt voor geschikt is, terwijl we hem zullen uitrusten met wat extra hardware die een en ander mogelijk kan maken.
Hier wordt een of meerdere komputerpoorten (8 tot 16 en zelfs 24 bits) gebruikt, om een digitaal signaal te leveren voor een zogenaamde DAC-chip. Dit is een digitaal-analoog-converter.
De principiele werking hiervan is erg eenvoudig in te zien.
Stel dat we een schakeling zo bouwen dat op een 8 bits poort van de komputer bit 0 wordt aangesloten op een schakelaar via een grote weerstand (stel=R ) een spanning U naar een belasting voert. Bit 1 schakelt eveneens een schakelaar die dezelfde spanning , maar nu via een weerstand die slechts half zo groot is ( R/2) naar dezelfde belasting voert. Bit 2, op dezelfde manier via een weerstand van R/4 , Bit 3 met R/8 , Bit 4 met R/16 , Bit 5 met R/32 , Bit 6 met R/64 en tenslotte Bit 7 met R/128.
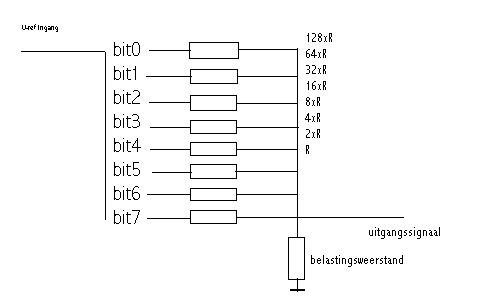
Bovenstaand schema moge de principiele werking van zo'n DAC schakeling verduidelijken. Elk bit zorgt van een andere waarde van de spanning die over de belastingsweerstand aan de uitgang zal verschijnen. Elke golfvorm, zolang hij maar uit niet meer dan 256 stapjes kan worden opgebouwd, is door het uitsturen van de gepaste bit-patronen bereikbaar. Bovendien is er een eenvoudig verband tussen de numerieke waarde van het uitgestuurde byte, en de momentane waarde van de opgewekte spanning.
Willen we op die manier een golfvorm synthetisch bereiken, dan moeten we net zoals voor PCM-modulatie over een nogal snelle komputer kunnen beschikken. Deze moet immers in staat zijn om minstens 40000 maal per sekonde een byte (bij 16-bit konverters dient dit een 'word' of twee bytes te zijn) naar de DAC te sturen, en moet daareenboven nog de tijd hebben om ook nog enkele zinnige algoritmes te berekenen die de golfvorm moeten bepalen.
Deze metode leent zich dan ook erg goed om gebruikt te worden in samenhang met zgn. dedicated-computersystemen , ofwel in een komputerarchitectuur die van parallel-processing gebruik maakt. In bijna alle praktische toepassingen op PC-nivo, wordt hiervoor gebruik gemaakt van supplementaire processoren, meestal DSP-chips (Digital Signal Processors) die speciaal zijn ontworpen voor dit soort toepassingen. (Bvb. de chips op een Sound Blaster kaart voor de ISA bus). Op de hardware van een en ander zullen we verder ingaan in het tweede hoofdstuk, waarbij de elektronika uit de doeken wordt gedaan.
Bij alle digitale vormen van klanksynthese moet rekening gehouden worden met het theorema van Shannon uit de wiskundige informatietheorie. Dit theorema stelt dat elke in bandbreedte begrensde golfvorm, volledig kan worden beschreven door de amplitude ervan aan minstens meer dan de dubbele frekwentie van de hoogste erin voorkomende komponent, te samplen. 'Samplen' is engels voor het nemen van een staal, d.w.z. het meten van de momentane waarde van een variabele. Een verzameling van dergelijke op regelmatige tijdstippen genomen stalen, noemt met eveneens een 'sample'.
In de muzikale praktijk komt een en ander erop neer, dat willen we het gehele audio frekwentiebereik kunnen bestrijken, de sampling rate, het dubbele moet zijn van de hoogste waarneembare toonhoogtekomponent. Zo komen we dan ook aan waarden tussen 33ks/s en 48ks/s (kilosamples per sekonde). (Cfr. Nyquist- theorema).
Deze vorm van klank-synthese maakt het mogelijk de komputer voor een belangrijk deel te ontlasten van de taak om op werkelijk elk ogenblik de golfvorm te bepalen. Hier wordt de komputer gebruikt om de samenhang tussen de diverse bepalende komponenten van een golfvorm algoritmisch te sturen. Het eigenlijke genereren van de resulterende klank wordt daarbij meestal overgelaten aan speciaal daartoe ontworpen schakelingen. FM-synthese staat voor Frekwentie Modulatie Synthese. Hierbij wordt een bepaalde basisgolfvorm in zijn frekwentie gemoduleerd door een modulatie-golfvorm. Dit kan nu worden herhaald, door die modulerende golfvorm op zijn beurt in frekwentie te moduleren enzovoort ...
Om de basis waarop FM-synthese berust goed te begrijpen, dienen we het principe van de ring-modulator goed te doorgronden. Dit is immers een schakeling (een dubbel gebalanceerde modulator heet dat in vakjargon) waarvan de overdrachtfunktie wiskundig vastligt alsvolgt :
Uout = Uxin * Uyin
De schakeling vermenigvuldigt dus de momentane waarde van de beide op de ingangen aangeboden spanningen. Wanneer je dit zou uitwerken voor twee zuiver sinusvormig verlopende spanningen van gelijke frekwentie en in dezelfde fase toegevoerd als Ux en Uy dan zal de frekwentie van Uout heel precies het dubbele zijn van die van de ingangssignalen.
(A*Sin(2p f.t)) * (A*Sin(2p f.t)) = [(A^2)*(1- Cos(2p 2f.t))]/ 2
of: (A*Sin(2p f.t))^2 = [(A^2)*(1- Cos(4p f.t))]/ 2
Merk op dat deze formule overeenkomt met een DC-komponent in het uitgangssignaal, veroorzaakt door de term 1-Cos() . Dit kan vermeden worden door de ingangssignalen onderling in faze te draaien. Wie zich nog zo'n beetje de goniometrie uit het sekundair onderwijs herinnert kent wellicht ook nog de formule:
Cos j * Sin j = (Sin 2j ) / 2
Zoals je ziet is de DC komponent hier weggevallen en krijgen we in het frekwentiedomein hetzelfde rezultaat als hiervoor: frekwentieverdubbeling.
Algemeen , en meer muzikaal uitgedrukt kunnen we stellen dat een ringmodulator alle som en verschiltonen tussen beide ingangsfrekwenties genereert. Het is duidelijk in te zien de bereikte golfvorm op de uitgang van de schakeling in eerste plaats afhangt van de frekwentieverhouding der ingangsspanningen evenals van hun golfvorm en onderlinge faseverhouding. Om een golfvorm vast te leggen in deze techniek volstaat het dan ook de relatie tussen beide ingangen vast te leggen en te programmeren. Deze relatie noemt men een algoritme voor klanksynthese. Om een praktisch inzicht te krijgen in het funktioneren van FM-synthese verdient het aanbeveling wat te spelen met het hiervoor afgedrukte programma, waarbij je dan wel in de menu-keuze , de optie FM- synthese dient te kiezen. Let erop dat het programma FM-synthese simuleert onder gebruikmaking van slechts 1 modulator en 1 draaggolf.( 1 operator). Je kan het echter makkelijk uitbreiden tot zoveel operatoren als gewenst.
Wanneer je het programma intypt en runt, zal je merken dat de komputer heel wat tijd nodig heeft voor de berekening, verwerking en (vooral) tekening van het resultaat. Dit moge reeds een vingerwijzing zijn die intuitief duidelijk moge maken welke snelheidseisen er zouden moeten gesteld worden aan een komputer die deze golfvormen in real-time zou moeten opwekken via zuiver digitale synthese!
De schakeling die de eigenlijke synthesizer vormt kan in werkelijkheid zowel zuiver digitaal als ook volkomen analoog worden opgebouwd. Ook kan , gebruik makend van komponenten uit de analoge elektronischemuziekstudiotechniek , een discrete FM-synthesizer worden opgebouwd. Ook de programmering ervan kan zowel gebruik maken van analoge als van digitale technieken Sedert zowat twintig jaar worden FM-synthesizers op de markt gebracht , hetzij als keyboard-synthesizers, hetzij in de vorm van stand-alone modules, die volledig vanuit een Midi-systeem geprogrammeerd kunnen worden. Aan zulke tuigen wil ik hier wat meer aandacht schenken.
Dergelijke kommercieel verkrijgbare FM-synthesizer modules en schakelingen zijn vaak opgebouwd uit 4 tot 16 operatoren, (ringmodulators ) terwijl men de manier waarop de modulatoren met elkaar verbonden worden (ten onrechte eigenlijk) algoritmen noemt. De ringmodulator die het uiteindelijk gebruikte uitgangssignaal levert, noemt men de 'carrier' ( cfr. draaggolf), alle andere zijn 'modulators'. Enkele mogelijke algoritmes eigenlijk had men dit veel beter 'patches' kunnen noemen ) voor bvb. de legendarische Yamaha DX21 FM-synthesizer zien eruit alsvolgt:
ALGORITME 1:
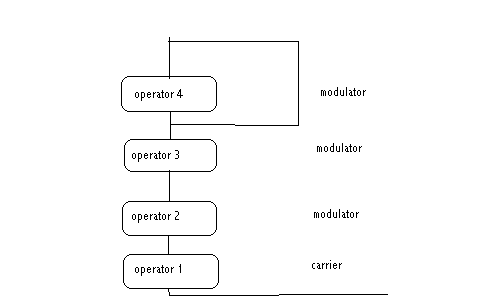
Merk op dat in nevenstaand algoritme (de term heeft alleen zin in zijn vertaling naar de erdoor geimplementeerde wiskundige funktie) de vierde operator voorzien is van een feedback-lus. Uiteraard is de mate van feedback hierbij programmeerbaar.
ALGORITME5:
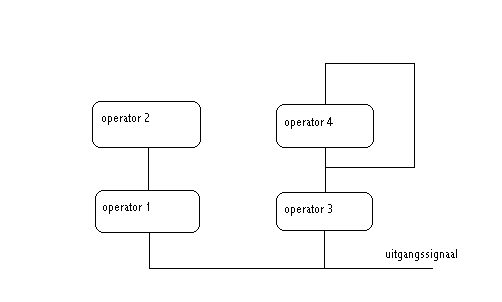
Merk op dat dit algoritme eigenlijk slechts 2 vermenigvuldigingen toepast en opgeteld worden. Eigenlijk hebben we dus reeds een menging van FM en een vorm van additieve synthese.
ALGORITME 8:
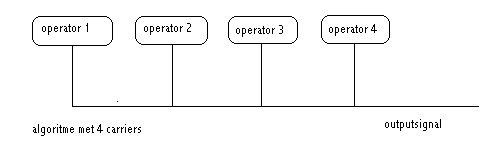
Ik wil dit voorbeeld ook nog geven omdat het eigenlijk helemaal geen FM- synthese algoritme meer is, maar eerder een voor louter additieve synthese , zoals duidelijk zal zijn uit het schema:
Modulatie van de operatoren is in dit geval helemaal niet mogelijk. De uitgangsgolf is gewoon de additieve som van de verschillende draaggolffrekwenties.
Uit het voorhanden zijn van dit algoritme in deze machine mag je echter niet besluiten dat het dus ook een volwaardige additieve synthesizer zou zijn! Immers, voor een goede additieve synthese zijn minimaal zowat 24 tot 50 komponenten nodig . De mogelijkheid om ook dit soort patches tot stand te brengen is alleen kommercieel ingegeven. De DX7 kwam immers op de markt toen de additieve synthese nog volop gangbaar was en men heeft iets van de oude tradities willen veilig stellen.
Parameters voor FM-klanksynthese :
Dit zijn de veranderlijken die voor FM-synthese kunnen worden ingesteld door de gebruiker ( programmeur). Welke parameters gebruikt kunnen worden is heel erg sterk afhankelijk van het soort machine dat gebruikt wordt .
1. Algoritme :
Dus in deze (eigenlijk foutieve) kontekst, de manier waarop de diverse modulatoren met elkaar worden gekoppeld en verbonden.
Voor de TX81Z, de DX21 enz... zijn er 8 verschillende algoritmes selekteerbaar.
Alle operatoren kunnen individueel aan of uitgeschakeld worden.
2. Frekwentieverhouding van de operatoren tot die van de carrier.
Niet de absolute frekwentie wordt geprogrammeerd dus, maar wel de interval-relatie tussen de diverse frekwenties van operatoren en draaggolven. Dit is een ernstige beperking, want voor een volledig vrije programmeerbaarheid moeten we elke denkbare relatie kunnen instellen. Op de DX21 kan voor elke operator gekozen worden uit 64 verschillende intervalverhoudingen ( van 0.5 tot 25.95).
Wanneer deze parameter wordt ingesteld voor de draaggolf, en men een normale toonhoogte van La=440Hz wil verkrijgen zonder enige transpositie, moet men deze parameter voor de draaggolf in elk geval op 1 stellen. 0.5 transponeert een oktaaf omlaag, 2 een oktaaf omhoog. Deze parameter bepaalt voor de draaggolf de basistoonhoogte, en toegepast op de operatoren, de klankkleur. Komplexe intervalverhoudingen voor de operatoren geven aanleiding tot non-harmonische klanken met een bijzonder rijk en breed uitgestrekt spektrum.
3. Omhullende van elke operator en van de carrier.
De omhullende of 'enveloppe' is het amplitudeverloop in de tijd van een golfvorm. De omhullende generator (wordt ook vaak ADSR genaamd , van Attack - Decay - Sustain - Release ) start zijn aktiviteit bij het begin van een klank.
De subparameters die met betrekking tot de omhullende van draaggolf of operator geprogrammeerd ( in dit voorbeeld is uitgegaan van de Yamaha DX21, omdat we zo'n machine in de klas hebben opgesteld ) kunnen worden zijn :
4.Toonhoogte-verloop of pitch-enveloppe :
dit zijn eventuele veranderingen in de toonhoogte van draaggolf of operator tijdens het verloop van de klank.
5.Feedback-niveau :
op de DX21 kan de mate waarin het uitgangssignaal van operator 4 teruggekoppeld wordt naar zijn eigen modulatieingang, ingesteld worden. ( waarden van 0 tot 7)
6.Amplitude-modulatie diepte
7.Low-frequency modulatie (LFO) , wat gebruikt wordt voor het bereiken van vibrato enzomeer , kan met niet minder dan zes parameters ingesteld worden :
- LFO -golfvorm :
- LFO- speed :
frekwentie van de LFO, regelbaar van 0.06 Hz tot 50 Hz. ( waarden van 0 tot 99)
- LFO-delay :
dit is de tijdsvertraging tussen het aanzetten van een klank en het inzetten van het LFO effekt. Dit is regelbaar van 0 tot 3 sekonden. Ook hier kunnen waarden ingevoerd worden van 0 tot 99.
- LFO-modulatiediepte :
deze parameter regelt de modulatiediepte van de LFO's werkzaam op alle gebruikte operatoren terzelfdertijd.
- LFO-amplitudemodulatie :
regelbaar van 0 tot 99 en werkzaam zoals de vorige parameter.
- LFO-sync :
deze parameter kan alleen aan of uit zijn, en bepaald of de LFO moet starten gesynchroniseerd met het inzetten van de klank, dan wel of hij alsmaar door moet oscilleren.
8.Toonhoogtemodulatiegevoeligheid ( pitch-modulation-sensitivity),
een parameter die de gevoeligheid van de operator instelt voor wijzigingen die gevolg zijn van het gebruik van een 'pmd' of, pitch-modulation device ( toonhoogtewielcontroller, wind- controller of iets dergelijks ).
9.Amplitudemodulatiegevoeligheid:
analoog, maar nu met betrekking tot amplitudemodulatie. (tremolo)
10. EG bias :
stelt de gevoeligheid van een operator of draaggolf in voor de effecten van een 'breath-controller'.
11.Key-velocity :
hiermee kan de mate waarin de waarde voor de noot-aanslag de operator beinvloedt worden ingesteld.
12.Operator outputlevel:
hiermee kan men de absolute sterkte instellen van het operator signaal dat als modulator wordt gebruikt. (0-99)
13.Rate scaling :
hiermee kan middels 0 of 1 bepaald worden of de toegepaste operatorparameters in verhouding tot de toonhoogte van de eindklank dienen te staan of niet. Het effekt hiervan is, dat bvb. indien deze parameter 1 is, vibrato's op hoge noten , sneller zullen worden gespeeld dan op lage noten.
14.Level scaling :
hiermee wordt een aan vorige parameter gelijk effekt ingesteld, maar dan met betrekking tot de absolute geluidsterkte der klanken. Hogere noten worden gradueel stiller gespeeld indien deze parameter 1 wordt gemaakt.
C.KLANKKLEURSYNTHESE VIA MIDI ...
de uiterste grenzen van het midi systeem.
Alle hiervoor onder FM-synthese beschreven parameters kunnen via MIDI-worden geprogrammeerd in zowat elke moderne FM-synthesizermodule. Begrijp echter goed dat een op die manier geprogrammeerde klank slechts kan worden gespeeld NADAT hij geprogrammeerd werd. Bovendien kan de FM- synthesizer terwijl hij een programmatiebevel via het midi-kanaal ontvangt, (in de meeste gevallen en bij de meeste machines) niet met het genereren van klanken bezig zijn. Het programmeren van een enkele klank vergt het versturen van tussen de 100 tot 500 midi-bytes vanuit de komputer naar de synthesizer, gebruik makend van een speciale routine met system-exclusives. Willen we een hele zgn. voice-bank herprogrammeren, dan vergt dit het uitsturen van niet minder dan 96 * 100 bytes =9600 bytes, wanneer er 96 klanken kunnen geprogrammeerd worden.
Zoals we zagen bij de introduktie van het Midi-systeem en zijn technische specifikaties, is de snelheid waarmee data kunnen worden overgedragen beperkt door de Baud-rate van het seriele systeem , nml. 31250 Baud. Brengen we hier eveneens in herinnering dat 1 Baud overeenkomt , in het geval van Midi-dataoverdracht, met 10 bits ( een midi-byte vraagt in het seriele formaat 10 bits). Een een eenvoudig rekensommetje leert ons dat er slechts 3125 bytes per sekonde kunnen overgedragen worden. De verzending van 500 midi bytes zal dan ook een tijdsduur van 500/3125 seconden duren in het allerbeste geval . De verzending van de data voor het herprogrammeren van een gehele voice-bank duurt zelfs 9600/3125=3 sekonden! Nu is zelfs 1/6 van een sekonde, muzikaal gesproken een duur die elke muzikale ritmiek reeds flink in 't honderd kan sturen.
Bovendien gaat een en ander in werkelijkheid nog een flink stuk trager, omdat de synthesizer zelf ook nog een zekere tijd nodig heeft voor de verwerking van de ontvangen gegevens. Deze tijd wordt evenwel door geen enkele mij bekende fabrikant, gepubliceerd. (Je merkt het snel genoeg...) Wat meestal wel voorzien is, is dat de Midi FM-synthesizer na ontvangst van een klanksynthese algoritme en de verwerking daarvan, zelf een Midi-signaal naar de komputer terugstuurt, als teken dat hij klaar is met de verwerking. De slimme programmeur en komponist zal natuurlijk in zijn programma van dit feit gebruik weten te maken om het onderste uit de Midi-kan te halen. Het door de synthesizer teruggestuurde byte noemt men een 'Acknowledge' bericht. Sommige synthesizers laten echter ook op het kleine schermpje het bericht verschijnen "Midi Dump Received", als signaal dat de gegevens aangekomen en verwerkt zijn.
Deze beperkingen maken dat het gebruik van klanksynthese in real- time, met Midi de absolute grenzen van het systeem raakt. Bovendien is het, gegeven de op de markt beschikbare apparatuur, a priori uitgesloten om bvb. middels Midi een klank weer te geven op een synthesizer en die vervolgens, terwijl hij klinkt en dus in real-time, in zijn interne samenstelling of mikrokompositie algoritmisch te wijzigen.
Via het gebruik van programmeerbare real-time controllers kan dit manko in beperkte mate worden gekompenseerd.
D. Digitale FM Synthese
Volgende paragraaf werd overgenomen uit de website van Barry Truax (cfr. links)
When the frequency of the modulator (which we'll call M) is in the sub-audio range (1-20 Hz), we can hear siren-like changes in pitch of the carrier. However, when we raise M to the audio range (above 30 Hz) then we hear a new timbre composed of frequencies called SIDEBANDS. To determine which sidebands are present, we have to control the ratio between the carrier frequency (C) and the modulating frequency (M). Instead of dealing with these frequencies in Hz, we'll refer to this relationship as the C : M RATIO, keeping C and M as integers.
Properties of C:M Ratios
First, about the properties of ratios, and some conventions we're using:
We will only deal with ratios that are called non-reducible, that is, those involving integers evenly divisible only by 1, and not by any other integer. For example, the ratio 2:2 is the same as 1:1 and can be reduced to it for all practical purposes. Likewise, 10:4 is the same as 5:2, and 9:6 is the same as 3:2, and so on.
Secondly, we're going to divide all possible ratios into some subgroups for ease of handling. One group will be those described as the 1:N ratios. This means ratios like 1:1, 1:2, 1:3, 1:4 etc. They will be found to have particular properties.
Another group will be those described as N:M where N,M are less than 10. In thise case, the restriction to single digit numbers is purely for ease of arithmetic calculation. The last group is called 'large number ratios', and this involves numbers 10 and up. Again, the division is arbitrary. We won't deal with ratios like 100:1 or 100:99. Those are legitimate ones and you can discover their properties through POD synthesis. C:M ratios are sometimes expressed with real numbers, e.g. the ratio 1:1.4, but these can be approximated by integers, in this case 5:7. In FM, a set of sidebands is produced around the carrier C, equally spaced at a distance equal to the modulating frequency M. Therefore, we often refer to the sidebands in pairs: 1st, 2nd, 3rd, and so on.
Calculating Sidebands
The so-called upper sidebands are those lying above the carrier. Their frequencies are:
C+M C+2M C+3M C+4M C+5M ....
For example, if C:M is 1:2, that is, the modulator is twice the frequency of the carrier, then the first upper sideband is: C+M = 1+2 = 3. The second upper sideband is: C+2M = 1+(2x2) = 1+4 = 5. Another way to get the second sideband is to add M=2 to the value of the first sideband which is 3; i.e. (C+M) + M = 3+2 = 5. It quickly becomes clear that the upper sidebands in this example are all the odd numbers, and since the carrier is 1, the upper sidebands are all the odd harmonics, with the carrier as the fundamental (i.e. the lowest frequency in the spectrum).
However, if our C:M were 2:5, the first upper sideband would be 2+5 = 7. Since 7 is not a multiple of 2, it would be termed inharmonic. But the second upper sideband would be 7+5 = 12, and that is the 6th harmonic. Therefore, we can see that sidebands can be harmonic or inharmonic.
The lower sidebands are: C-M C-2M C-3M C-4M C-5M ...
When the sideband is a positive number it will lie below the carrier, but at some point, its value will become negative. It is then said to be reflected because we simply drop the minus sign and treat it as a positive number, e.g. the sideband -3 appears in the spectrum as 3. Acoustically, however, this reflected process involves a phase inversion, i.e. the spectral component is 180 degrees out of phase. Mathematically, we express this reflection by using absolute value signs around the expression: /C-M/ to indicate that we drop the minus and treat the number as positive.
For example, for 1:2, the 1st lower sideband is: /C-M/ = /1-2/ = /-1/ =1.
The second lower sideband is: /C-2M/ = /1-(2x2)/ = /1-4/ = /-3/ = 3. However, to make things easier, we could have added 2 to the first lower sideband (1), which is already reflected, and have obtained 3.
For the ratio 1:1, the 1st lower sideband is 0 (inaudible) and the 2nd, 3rd and 4th lower sidebands are 1, 2, 3, respectively.
For 7:5, the lower sidebands are: 2 3 8 13 where 3 is the 1st reflected one. One concern we have in using a given C:M ratio is whether the carrier frequency is the lowest frequency in the spectrum, i.e. is it the fundamental? If it is, we can treat the carrier frequency as the principal pitch that will be heard in the resulting timbre.
First we have the case of the 1:1 ratio whose upper sidebands are 2,3,4,... and whose lower sidebands are 0,1,2,3,... Clearly the carrier is the lowest non-zero component, and all the sidebands are harmonics, i.e. multiples. Because 1:1 is the only ratio with a zero lower sideband, it is a special case. It is also the only ratio producing the entire harmonic series. For other ratios, we could work out their sidebands and decide if any of them were lower than the carrier. That is fine, but tedious, and we'd like to know in advance what to expect. First, we might note that in the 1:2 case the 1st lower sideband is /-1/ = 1; therefore it fell against the carrier. Further, if M is larger than twice C, e.g. 2:5, then the 1st reflected sideband will always be greater than the carrier.
Work out a few examples and you'll find that the rule is:
FOR THE CARRIER TO BE THE FUNDAMENTAL: M MUST BE GREATER THAN OR EQUAL TO TWICE C, OR ELSE BE THE 1:1 RATIO.
Another useful property to be familiar with is the occurrence, as you may have noticed already, of lower sidebands coinciding with the upper set. They are said to 'fall against' them.
What this means acoustically is that the amplitudes of the two sidebands will add together, influenced as well by the phase inversion of the reflected sideband. Since the amplitude of each sideband varies according to the strength of the modulation, as expressed by the Modulation Index, the sum of the contributions of each sideband becomes quite complex!
You've probably noticed that the sidebands of the 1:1 ratio have this property of falling against each other. You'll find a very similar pattern with all of the N:1 ratios, i.e. 2:1, 3:1, 4:1, 5:1 ...
The second type of ratio showing the same property is that like 1:2. The odd harmonics are found in both the upper and lower sidebands. Therefore we can extrapolate the second case, namely odd N:2, that is, the ratios 1:2, 3:2, 5:2, 7:2 ...
No other ratios except N:1 and odd N:2 have this property. All ratios other than N:1 and odd N:2 have an asymmetrical spacing of their sidebands. That is, the distance in frequency between adjacent sidebands is unequal. For instance, the ratio 2:5 with its sidebands 2 3 7 8 12 .... However, there is still a pattern to the spacing.
We want the distance between the first upper sideband (C + M) and the first reflected lower sideband (C - M) which is negative by definition and therefore can be made positive to give the expression (M - C). Subtract these two frequencies to get: (C + M) - (M - C) = 2C We find that the answer is 2C. Since the spacing of all upper or lower sidebands is M, then the remaining spacing is M - 2C.
Therefore the rule is:
WHEN C IS THE LOWEST FREQUENCY IN THE SPECTRUM, THE SPACING OF SIDEBANDS ABOVE IT (EXCEPT FOR 1:1) WILL BE: M - 2.C & 2.C
For the above example (2:5), the spacing is 2x2=4 and 5-4=1. Note that we have to start with C as the fundamental. This will be referred to in the next section as the Normal Form of the Ratio.
Normal Form of the C:M Ratio
Definition: a C:M ratio is in Normal Form (N.F.) when the carrier is the fundamental in the spectrum it produces.
Rule: for a ratio to be in Normal Form, M must be greater than or equal to twice C, or else be the ratio 1:1
What we are doing with the concept of Normal Form is providing the basis of a classification scheme for all ratios, and at the same time codifying our rule of thumb about the conditions for the carrier to be the fundamental. If we consider only ratios involving integers up to 9, we can list all those in Normal Form:
1:1 1:2 4:9 3:7 2:5 3:8 1:3 2:7 1:4 2:9 1:5 1:6 1:7 1:8 1:9
These have been listed in an order related to what's called the Farey Series where the value of M/C is increasing, or C/M is decreasing. Each N.F. ratio will have associated with it a family of ratios, as shown below.
Reducing a Non Normal Form Ratio to its Normal Form
When the M value in a ratio is less than twice the C value, it is not in Normal Form, but can be reduced to it by applying the operation:
C = /C - M/
What this means is that you subtract M from C (ignoring any minus sign) and treat the result as the new C value. You keep doing this until the ratio satisfies the Normal Form criterion.
Consider, for example, the ratio 3:1. We first take 3-1=2 and get the ratio 2:1, which is still not in Normal Form. Another application of the operation gives us 2-1=1 and the ratio 1:1 which is in Normal Form by definition.
A trickier example is 8:5. First we reduce 8-5=3 and get 3:5 (not N.F.) Reducing again, we get 3-5=-2, which becomes 2:5 (ignoring the minus!) and because 5 is greater than twice 2, we have a Normal Form ratio. Notice that the reduction operation is the reverse of generating sidebands.
To generate sidebands we add M to C; to reduce the ratio, we subtract.
Families of C:M Ratios
For each Normal Form ratio there exists a set of ratios which produce the same set of sidebands. We'll call this set of ratios a 'family', and identify the family by its Normal Form ratio.
Consider the ratios 2:5, 3:5 and 7:5. Here are their sidebands:
2:5 2 3 7 8 12 13 17 18 22 23 27 28
3:5 3 2 8 7 13 12 18 17 23 22 28 27
7:5 7 2 12 3 17 8 22 13 27 18 32 23
We can see that all 3 ratios produce the same sidebands but in a different order. 2:5 is the Normal Form ratio and so this is the 2:5 family. How can we generate the entire set of family members? The rule is:
For a C:M ratio in Normal Form, the set of family members is:
C + N.M : M & /C - N.M/ : M for N=1,2,3,4,...
We simply take each sideband in turn and use it as the C value of the ratio, keeping M constant. The 2:5 family is 3:5,7:5,8:5,12:5,13:5,17:5,18:5,...
Harmonic & Inharmonic C:M Ratios
When we showed how to generate sidebands, we noted that some were harmonic and some were inharmonic (i.e. not multiples of the fundamental). Acoustically, this is an important distinction because each ratio produces an inharmonic or inharmonic timbre - a property usable compositionally.
The rule for determining harmonic/inharmonic is easy for Normal Form Ratios:
Harmonic N.F. ratios are always of the form 1:N, and inharmonic ones aren't.
Harmonic Ratios: 1:1 1:2 1:3 1:4 1:5 1:6 1:7 1:8 1:9
Inharmonic Ratios: 2:9 2:7 3:8 2:5 2:7 4:9
When a ratio is not in Normal Form, and you want to know if it is harmonic or not, you can reduce it to Normal Form & find out. However, ratios with M = 1,2,3,4,6 are always harmonic; for M=5,7,8,9 check if C is a multiple of M plus or minus 1; if so, it's harmonic. For instance, 9:5, 11:5, 14:5 and 16:5 are members of the 1:5 family whose C values are 10-1,10+1,15-1,15+1.
Calculating The Fundamental Frequency
On the other hand, 2:5 family members are 7:5, 8:5, 12:5, 13:5 & are inharmonic. Once we are thinking along the lines of families of ratios producing the same set of sidebands, we may want to know how to calculate the right carrier frequency for a family member ratio that produces the same spectrum as the Normal Form ratio on a given fundamental-carrier, e.g. 100 Hz for ease of calculation. In the PODX system this can be done for you automatically when you ask for the frequencies to be treated as modulators (note: M is constant for a family. To do the calculation yourself, take a Normal Form ratio NFC:M with a given carrier frequency. Then for a given family member ratio C:M, what should its carrier frequency (FC) be to keep the fundamental the same?
The equation is:
FC = (C ratio) x (N.F. Carrier freq.) / (N.F. C ratio)
For example, if the N.F. carrier frequency is 100 Hz. for 1:1, then the corresponding carrier for 3:1 is (3x100/1) = 300 Hz. For any 1:N ratio we can get the answer by taking C x 100. For a NFC:M ratio, we take C x 100 / NFC, e.g. for 7:5 and 2:5, the carrier for 7:5 is 7x100/2 = 350 Hz. Acoustically we hear a non N.F. family member on a high carrier as having its energy distributed around high partials, rather than centred on the fundamental, at least for a low modulation index.
When we use a non Normal Form ratio with a specific carrier frequency, we often want to know what is its fundamental frequency, or we wish a specific fundamental and want to know how to calculate the appropriate carrier. This is done for you in PODX when you request that the frequency be treated as the fundamental. The program calculates the right carrier to produce the fundamental that is required.
To calculate the fundamental (FF) for a non Normal Form ratio C:M whose carrier is known, we need to know the Normal Form of the ratio NFC:M, and then we can use the equation:
FF = (Carrier frequency) x (N.F. C ratio) / (C ratio)
For example, with 5:2 and a carrier of 500 Hz, the Normal Form ratio is 1:2 and therefore the fundamental is (500 x 1 / 5) = 100 Hz. Similarly, for 7:5 and a carrier of 700 Hz., the Normal Form ratio is 2:5, and therefore the fundamental is (700 x 2 / 7) = 200 Hz.
If we know the fundamental and need the carrier, we can use the equation:
Carrier = (Fundamental) / (C ratio) / (N.F. C ratio)
References:
B. Truax, "Organizational Techniques for C:M Ratios in Frequency Modulation", Computer Music Journal, 1(4), 1978, pp. 39-45; reprinted in Foundations of Computer Music, C. Roads and J. Strawn (eds.). MIT Press, 1985.
J. Chowning, "The Synthesis of Complex Audio Spectra by Means of Frequency Modulation," Journal of the Audio Engineering Society 21(7), 1973; reprinted in Computer Music Journal 1(2), 1977.
B. Schottstaedt, "The Simulation of Natural Instrument Tones Using Frequency Modulation with a Complex Modulating Wave," Computer Music Journal 1(4), 1977.
J. Bate, "The Effects of Modulator Phase on Timbres in FM Synthesis," Computer Music Journal 14(3), 1990.
F. Holm, "Understanding FM Implementations: A Call for Common Standards," Computer Music Journal 16(1), 1992.
E. Granular Synthesis
Sedert versie 5.00 van <GMT> staan funkties voor real time granulaire synthese ter beschikking binnen de library. Kode voorbeelden en konkrete real time toepassingen kunnen weergevonden worden in de source kode voor stukken zoals <Fidel-C> (voor viool en komputer).
Volgende paragraaf, waarin het principe van de granulaire synteze wordt uitgelegd, werd overgenomen uit de website van Barry Truax (cfr. links).
Granular synthesis was first suggested as a computer music technique for producing complex sounds by Iannis Xenakis (1971) and Curtis Roads (1978) and is based on the production of a high density of small acoustic events called 'grains' that are less than 50 ms in duration and typically in the range of 10-30 ms. Typical grain densities range from several hundred to several thousand grains per second where the grain itself may come from a wavetable (e.g. sine wave), FM synthesis or sampled sound. Such high densities of events made the technique difficult to work with because of the large amount of calculation required, and therefore until recently few composers have experimented with it. Using a digital signal processor controlled by a microcomputer, Barry Truax implemented the technique with real-time synthesis in 1986 and incorporated it within an interactive compositional environment, the PODX system, at Simon Fraser University. This technique was exclusively used to realize his work Riverrun.
What is most remarkable about the technique is the relation between the triviality of the grain (heard alone it is the merest click or 'point' of sound) and the richness of the layered granular texture that results from their superimposition. The grain is an example of British physicist Dennis Gabor's idea (proposed in 1947) of the quantum of sound, an indivisible unit of information from the psychoacoustic point of view, on the basis of which all macro-level phenomena are based. In another analogy to quantum physics, time is reversible at the quantum level in that the quantum grain of sound is reversible with no change in perceptual quality. That is, if a granular synthesis texture is played backwards it will sound the same, just as if the direction of the individual grain is reversed (even if it is derived from natural sound), it sounds the same. This time invariance also permits a time shifting of sampled environmental sound, allowing it to be slowed down with no change in pitch. This technique is usually called granulation.
References:
De Poli, G., Piccialli, A. & Roads, C. (1991) Editors. Representations of Musical Signals. Cambridge, MA: The MIT Press
Gabor, D. (1947) Acoustical quanta and the theory of hearing. Nature, 159(4044), 591-594
Truax, B. (1988) Real-time granular synthesis with a digital signal processor. Computer Music Journal, 12(2), 14-26
F.Het komponeren van klanken en geluiden
In de traditionele opvatting van muzikale kompositie, is de komponist iemand die de bestaande instrumenten met hun gegeven klankkleuren en mogelijkheden gebruikt om een bepaalde muzikale gebeurtenis op te zetten. Zijn hele aandacht is gericht op zaken zoals samenhang tussen toonhoogtes, dynamiek, vormopbouw, ritmische structurering enzomeer...
De meer experimenteel ingestelde komponist daareentegen, beschikt over de mogelijkheid onnoemelijk veel verder en dieper te boren in de mogelijkheden van het muzikale medium. Hij hoeft zich immers niet zomaar neer te leggen bij het nu eenmaal gegeven zijn van de klanken, maar is integendeel in staat ook de klanken zelf in hun innerlijke struktuur, samen met andere microtemporele eigenschappen van de geluiden, te bepalen en/of te komponeren. De neiging om dit te doen is overigens niet alleen eigen aan musici uit de experimentele muziek die zich toeleggen op de elektronische media. Neen, ook die musici wier werk draait rond het zuiver akoestische interesseren zich veelal diepgaand aan dit perspektief. Velen gaan dan ook over tot het zelf ontwerpen van akoestische instrumenten en/of klankbronnen.(Meer daarover in boekdeel 4 gewijd aan organologie en experimentele instrumentenbouw).
Je zou het een beetje kunnen vergelijken met de schilder enerzijds, die slechts kleurtjes-recht-uit-het-potje zou gebruiken (en dit is dan de 'traditionele' komponist natuurlijk) tegenover anderzijds de schilder die zijn kleuren zelf samenstelt en over een persoonlijk palet beschikt.
Gebruikelijke soundkaarten voor Wintel PC's kunnen sample gegevens opslaan naar keuze als 16-bit getallen of 8 bit getallen. Soms worden we gekonfronteerd met konversie problemen. Daarom deze korte nota:
Konversie van 8-bit samples naar 16-bit samples zoals verworven door Sound-blaster kaarten
Gegevens:
16-bit samples hebben 8 extra bits aan de LSB kant.
16-bit samples worden opgeslagen als 'signed-integers'. Hun numeriek bereik loopt dus van -32768 to +32767, terwijl 8-bit samples geen teken hebben en dus lopen over een bereik van 0 tot 255.
Konversie van 16-bit samples naar 8-bit kan eenvoudig gebeuren via volgende procedure:
Stel B% is een 16-bit sample
Of in basic-kode:
IF B% < 0 THEN B% = ABS(B% ) ELSE B% = B% + &H80 :' omkering van het hoogste bit
Voor de omzetting van 8-bit samples naar 16 bit samples gaan we andersom tewerk:
Of in basic-kode:
Terloops wijzen we erop dat er voor sample rate konversies ook kan overwogen worden hardware oplossingen toe te passen. Verschillende fabrikanten hebben immers chips in hun leveringsprogramma waarmee bvb. eender welke input sample rate tussen 5ks/S en 250ks/S kan worden omgezet naar eender welke sample rate voor de output.
Filedate: [881217 / 920315/ 9709/ 0004/0101]/ June 8, 2010
| Terug naar inhoudstafel kursus: <Index Kursus> | Naar homepage dr.Godfried-Willem RAES | Naar Fourier analyze |